题目内容
如图,已知直线l1:y=-x+2与直线l2:y=2x+8相交于点F,l1、l2分别交x轴于点E、G,矩形ABCD顶点C、D分别在直线l1、l2,顶点A、B都在x轴上,且点B与点G重合。
(1)求点F的坐标和∠GEF的度数;
(2)求矩形ABCD的边DC与BC的长;
(3)若矩形ABCD从原地出发,沿x轴正方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤6)秒,矩形ABCD与△GEF重叠部分的面积为s,求s关于t的函数关系式,并写出相应的t的取值范围。
(1)求点F的坐标和∠GEF的度数;
(2)求矩形ABCD的边DC与BC的长;
(3)若矩形ABCD从原地出发,沿x轴正方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤6)秒,矩形ABCD与△GEF重叠部分的面积为s,求s关于t的函数关系式,并写出相应的t的取值范围。

解:(1)由题意得 ,
,
解得x=-2,y=4,
∴F点坐标:(-2,4);
过F点作直线FM垂直X轴交x轴于M,
ME=MF=4,△MEF是等腰直角三角形,∠GEF=45°;
(2)由图可知G点的坐标为(-4,0),则C点的横坐标为-4,
∵点C在直线l1上,
∴点C的坐标为(-4,6),
∵由图可知点D与点C的纵坐标相同,且点D在直线l2上,
∴点D的坐标为(-1,6),
∵由图可知点A与点D的横坐标相同,且点A在x轴上,
∴点A的坐标为(-1,0),
∴DC=|-1-(-4)|=3,BC=6;
(3)∵点E是l1与x轴的交点,
∴点E的坐标为(2,0),
S△GFE= =
= =12,
=12,
若矩形ABCD从原地出发,沿x轴正方向以每秒1个单位长度的速度平移,
当t秒时,移动的距离是1×t=t,
则B点的坐标为(-4+t,0),A点的坐标为(-1+t,0);
①在运动到t秒,若BC边与l2相交设交点为N,
AD与l1相交设交点为K,那么-4≤-4+t≤-2,
即0≤t≤2时.N点的坐标为(-4+t,2t),K点的坐标为(-1+t,3-t),
S=S△GFE-S△GNB-S△AEK=12- =
= ,
,
②在运动到t秒,若BC边与l1相交设交点为N,
AD与l1相交设交点为K,那么-2<-4+t且-1+t≤3,
即2<t≤4时,N点的坐标为(-4+t,6-t),K点的坐标为(-1+t,3-t),
S=S梯形BNKA= =
= ,
,
③在运动到t秒,若BC边与l1相交设交点为N,
AD与l1不相交,那么-4+t≤3且﹣1+t>3,
即4<t≤7时,N点的坐标为(-4+t,6-t),
S=S△BNE= =
= ,
,
答:(1)F点坐标:(-2,4),∠GEF的度数是45°;
(2)矩形ABCD的边DC的长为3,BC的长为6;
(3)s关于t的函数关系式 。
。
 ,
,解得x=-2,y=4,
∴F点坐标:(-2,4);
过F点作直线FM垂直X轴交x轴于M,
ME=MF=4,△MEF是等腰直角三角形,∠GEF=45°;
(2)由图可知G点的坐标为(-4,0),则C点的横坐标为-4,
∵点C在直线l1上,
∴点C的坐标为(-4,6),
∵由图可知点D与点C的纵坐标相同,且点D在直线l2上,
∴点D的坐标为(-1,6),
∵由图可知点A与点D的横坐标相同,且点A在x轴上,
∴点A的坐标为(-1,0),
∴DC=|-1-(-4)|=3,BC=6;
(3)∵点E是l1与x轴的交点,
∴点E的坐标为(2,0),
S△GFE=
 =
= =12,
=12,若矩形ABCD从原地出发,沿x轴正方向以每秒1个单位长度的速度平移,
当t秒时,移动的距离是1×t=t,
则B点的坐标为(-4+t,0),A点的坐标为(-1+t,0);
①在运动到t秒,若BC边与l2相交设交点为N,
AD与l1相交设交点为K,那么-4≤-4+t≤-2,
即0≤t≤2时.N点的坐标为(-4+t,2t),K点的坐标为(-1+t,3-t),
S=S△GFE-S△GNB-S△AEK=12-
 =
= ,
,②在运动到t秒,若BC边与l1相交设交点为N,
AD与l1相交设交点为K,那么-2<-4+t且-1+t≤3,
即2<t≤4时,N点的坐标为(-4+t,6-t),K点的坐标为(-1+t,3-t),
S=S梯形BNKA=
 =
= ,
,③在运动到t秒,若BC边与l1相交设交点为N,
AD与l1不相交,那么-4+t≤3且﹣1+t>3,
即4<t≤7时,N点的坐标为(-4+t,6-t),
S=S△BNE=
 =
= ,
,答:(1)F点坐标:(-2,4),∠GEF的度数是45°;
(2)矩形ABCD的边DC的长为3,BC的长为6;
(3)s关于t的函数关系式
 。
。
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( )
6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( ) (2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
(2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )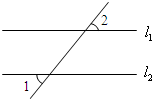 (2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2=
(2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2= 如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.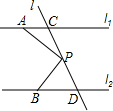 如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.