题目内容
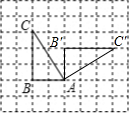
如图，方格纸中每个小正方形的边长均为1，△ABC的顶点均在小正方形的顶点处．
（1）以点A为旋转中心，把△ABC顺时针旋转90°，画出旋转后的△AB′C′；
（2）在（1）的条件下，求点C运动到点C′所经过的路径长．
解：（1）如图所示：
；
（2）∵AC=
=
，
∴点C运动到点C′所经过的路径为：
=
=
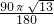π，
即点C运动到点C′所经过的路径长为π．
分析：（1）将△ABC的各顶点绕点C顺时针旋转90°后找到对应顶点，顺次连接得△AB′C′；
（2）点C运动到点C′所经过的路线是半径为AC，圆心角是90°的扇形的弧长．
点评：本题考查了利用旋转变换作图以及弧长的计算，熟练掌握网格结构并准确找出对应点的位置是解题的关键，注意掌握弧长公式：l=．
；（2）∵AC=
=，∴点C运动到点C′所经过的路径为：
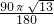==π，即点C运动到点C′所经过的路径长为
π．分析：（1）将△ABC的各顶点绕点C顺时针旋转90°后找到对应顶点，顺次连接得△AB′C′；
（2）点C运动到点C′所经过的路线是半径为AC，圆心角是90°的扇形的弧长．
点评：本题考查了利用旋转变换作图以及弧长的计算，熟练掌握网格结构并准确找出对应点的位置是解题的关键，注意掌握弧长公式：l=
． 
练习册系列答案
阅读快车系列答案
相关题目
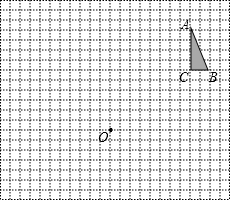如图，方格纸中每个小正方形的边长都是单位1．
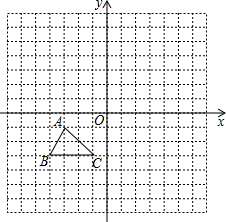系后，△ABC的顶点在格点上，点B的坐标为（-4．-3）．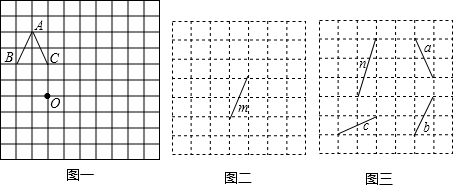
如图，方格纸中每个小正方形的边长都是单位1，△ABC和点S的位置如图所示．