题目内容
 (2012•大兴区二模)甲、乙两人同时从某地A出发,甲以60米/分钟的速度沿北偏东30°方向行走,乙沿北偏西45°方向行走,10分钟后甲到达B点,乙正好到达甲的正西方向的C点,此时甲、乙两人之间的距离是多少米?
(2012•大兴区二模)甲、乙两人同时从某地A出发,甲以60米/分钟的速度沿北偏东30°方向行走,乙沿北偏西45°方向行走,10分钟后甲到达B点,乙正好到达甲的正西方向的C点,此时甲、乙两人之间的距离是多少米?分析:过A作AD⊥BC交BC于D,则所求BC=CD+BD.先解直角△ABD,求出BD、AD的长,再解直角△ACD,求出CD的长.
解答: 解:过A作AD⊥BC交BC于D,则∠BAD=30°,∠CAD=45°.
解:过A作AD⊥BC交BC于D,则∠BAD=30°,∠CAD=45°.
∵AD⊥BC,
∴∠ADB=90°,∠ADC=90°.
在直角△ABD中,∵∠BAD=30°,∠ADB=90°,AB=60×10=600,
∴BD=
AB=300,AD=ABcos∠DAB=600×cos30°=300
.
在直角△ACD中,∵∠ADC=90°,∠CAD=45°,AD=300
,
∴CD=AD=300
.
∵BC=CD+BD,
∴BC=300
+300.
答:甲乙两人之间的距离是(300
+300)米.
 解:过A作AD⊥BC交BC于D,则∠BAD=30°,∠CAD=45°.
解:过A作AD⊥BC交BC于D,则∠BAD=30°,∠CAD=45°.∵AD⊥BC,
∴∠ADB=90°,∠ADC=90°.
在直角△ABD中,∵∠BAD=30°,∠ADB=90°,AB=60×10=600,
∴BD=
| 1 |
| 2 |
| 3 |
在直角△ACD中,∵∠ADC=90°,∠CAD=45°,AD=300
| 3 |
∴CD=AD=300
| 3 |
∵BC=CD+BD,
∴BC=300
| 3 |
答:甲乙两人之间的距离是(300
| 3 |
点评:本题主要考查的是解直角三角形的应用-方向角问题及解直角三角形,理解方向角的定义是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (2012•大兴区二模)已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
(2012•大兴区二模)已知二次函数y=ax2+bx+2,它的图象经过点(1,2).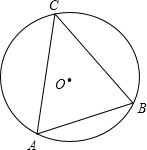 (2012•大兴区二模)如图,⊙O的半径为6,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是
(2012•大兴区二模)如图,⊙O的半径为6,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是