题目内容
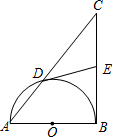 如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-10x+24=0的两个根,则DE的长为________.
如图,以△ABC的直角边AB为直径的半圆O与斜边AC交于点D,E是BC边的中点.若AD、AB的长是方程x2-10x+24=0的两个根,则DE的长为________.


分析:首先连接BD,由AB为直径,易证得△ABC∽△ADB,又由AD、AB的长是方程x2-10x+24=0的两个根,即可求得AD与AB的长,然后由相似三角形的对应边成比例,即可求得AC的长,然后由勾股定理求得BC的长,又由E是BC边的中点,即可求得DE的长.
解答:
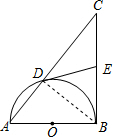 解:连接BD,
解:连接BD,∵AB为直径,
∴∠ADB=∠BDC=∠ABC=90°,
∵∠A是公共角,
∴△ABC∽△ADB,
∴
 ,
,∵AD、AB的长是方程x2-10x+24=0的个根,AB为圆的直径,
∴AD=4,AB=6,
∴AC=
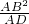 =
=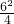 =9,
=9,∴BC=
 =3
=3 ,
,∵E是BC边的中点,
∴DE=
 BC=
BC=
 .
.故答案为:
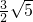 .
.点评:此题考查了相似三角形的判定与性质、圆周角定理、一元二次方程的解法以及直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
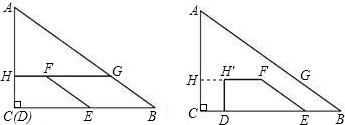
 23、如图是9×7的正方形点阵,其水平方向和竖直方向相邻的两格点间的长度都是1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:
23、如图是9×7的正方形点阵,其水平方向和竖直方向相邻的两格点间的长度都是1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题: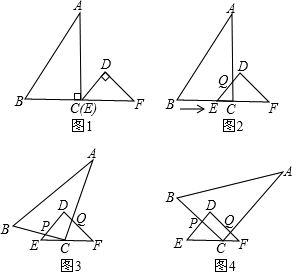 已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
