题目内容
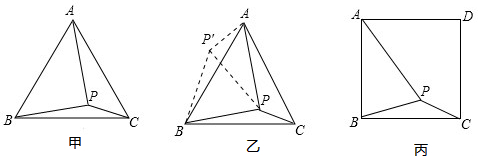
(1)如图甲,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于点D1,求∠BD1C的度数;
(2)如图乙,在图甲中再作∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是______.

解:(1)∵在△ABC中,∠A=52°,
∴∠ABC+∠ACB=180°-52°=128°,
∵∠ABC与∠ACB的角平分线交于点D1,
∴∠D1BC+∠D1CB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×128°=64°,
×128°=64°,
∴∠BD1C=180°-64°=116°;
(2)∵由(1)可知,∠BD1C=180°-64°=116°,
∴同理∠BD2C=180°- (∠ABC+∠ACB)=180°-96°=84°,
(∠ABC+∠ACB)=180°-96°=84°,
依此类推,∠BD5C=180°-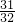 (∠ABC+∠ACB)=180°-124°=56°.
(∠ABC+∠ACB)=180°-124°=56°.
故答案为:56°.
分析:(1)先根据三角形内角和定理得出∠ABC+∠ACB的度数,再由角平分线的定义得出∠D1BC+∠D1CB的度数,根据三角形内角和定理即可得出结论;
(2)根据(1)中的结论找出规律即可得出结论.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.
∴∠ABC+∠ACB=180°-52°=128°,
∵∠ABC与∠ACB的角平分线交于点D1,
∴∠D1BC+∠D1CB=
 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×128°=64°,
×128°=64°,∴∠BD1C=180°-64°=116°;
(2)∵由(1)可知,∠BD1C=180°-64°=116°,
∴同理∠BD2C=180°-
 (∠ABC+∠ACB)=180°-96°=84°,
(∠ABC+∠ACB)=180°-96°=84°,依此类推,∠BD5C=180°-
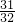 (∠ABC+∠ACB)=180°-124°=56°.
(∠ABC+∠ACB)=180°-124°=56°.故答案为:56°.
分析:(1)先根据三角形内角和定理得出∠ABC+∠ACB的度数,再由角平分线的定义得出∠D1BC+∠D1CB的度数,根据三角形内角和定理即可得出结论;
(2)根据(1)中的结论找出规律即可得出结论.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目