题目内容
如图,抛物线y=x2-2x-3与坐标轴交于A(-1,0)、B(3,0)、C(0,-3)三点,D为顶点.(1)D点坐标为(______,______).
(2)BC=______

【答案】分析:(1)直接利用抛物线的顶点公式即可得出D点的坐标;
(2)结合题意,可知可得出B点、C点和点D点的坐标,即可分别得出三个线段的长度,利用向量关系易得,BC⊥CD,即△BCD为直角三角形;
(3)假设存在这样的点P,经分析,有以下几种情况:①连接AC,可知Rt△COA∽Rt△BCD,②过A作AP1⊥AC交y轴于P1,可知Rt△CAP1∽Rt△BCD;③过4C作CP2⊥AC,交x轴于P2
可知Rt△P2CA∽Rt△BCD;结合上述情况,分别可得出对应的P的坐标;
解答: 解:(1)D(1,-4)(2分)
解:(1)D(1,-4)(2分)
(2)结合题意,可得C(0,-3);B(3,0)
 ,BD=2
,BD=2 ,CD=
,CD= ,
,
且 =(3,1),
=(3,1), =(1,-3),
=(1,-3),
可知 ,
,
即△BCD是直角三角形 (6分)
(3)①连接AC,可知Rt△COA∽Rt△BCD,符合条件的点为O(0,0)
②过A作AP1⊥AC交y轴于P1
可知Rt△CAP1∽Rt△BCD符合条件的点为
③过C作CP2⊥AC,交x轴于P2
可知Rt△P2CA∽Rt△BCD,符合条件的点为P2(9,0)
∴符合条件的点有三个:O(0,0), ,P2(9,0)(12分)
,P2(9,0)(12分)
点评:本题主要考查了抛物线方程的顶点公式和相似三角形的判定等知识点,有一定的综合性.
(2)结合题意,可知可得出B点、C点和点D点的坐标,即可分别得出三个线段的长度,利用向量关系易得,BC⊥CD,即△BCD为直角三角形;
(3)假设存在这样的点P,经分析,有以下几种情况:①连接AC,可知Rt△COA∽Rt△BCD,②过A作AP1⊥AC交y轴于P1,可知Rt△CAP1∽Rt△BCD;③过4C作CP2⊥AC,交x轴于P2
可知Rt△P2CA∽Rt△BCD;结合上述情况,分别可得出对应的P的坐标;
解答:
 解:(1)D(1,-4)(2分)
解:(1)D(1,-4)(2分)(2)结合题意,可得C(0,-3);B(3,0)
 ,BD=2
,BD=2 ,CD=
,CD= ,
,且
 =(3,1),
=(3,1), =(1,-3),
=(1,-3),可知
 ,
,即△BCD是直角三角形 (6分)
(3)①连接AC,可知Rt△COA∽Rt△BCD,符合条件的点为O(0,0)
②过A作AP1⊥AC交y轴于P1
可知Rt△CAP1∽Rt△BCD符合条件的点为

③过C作CP2⊥AC,交x轴于P2
可知Rt△P2CA∽Rt△BCD,符合条件的点为P2(9,0)
∴符合条件的点有三个:O(0,0),
 ,P2(9,0)(12分)
,P2(9,0)(12分)点评:本题主要考查了抛物线方程的顶点公式和相似三角形的判定等知识点,有一定的综合性.

练习册系列答案
相关题目
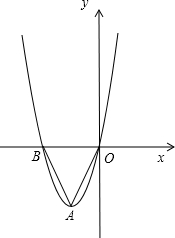 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO. 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l. (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.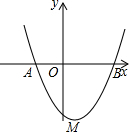 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.