题目内容
如图，沿AC方向开山修路，为加快施工进度，要在小山的另一边同时施工，从AC上的一点B取∠ABD=120°，BD=210m，∠D=30°，要正好能使A、C、E成一直线，那么E、D两点的距离等于
- A.105
m - B.210m
- C.70m
- D.105m
A
分析：连接ED，根据三角形内角与外角的关系可求出∠AED的度数，再根据勾股定理即可求出DE的长．
解答：
解：连接ED，可得∠AED=120°-30°=90°，
故在Rt△ADE中，∠AED=90°，BD=210m，∠D=30°，
解可得DE=105．
故选A．
点评：本题考查三角形的外角性质与勾股定理的应用．
分析：连接ED，根据三角形内角与外角的关系可求出∠AED的度数，再根据勾股定理即可求出DE的长．
解答：
解：连接ED，可得∠AED=120°-30°=90°，故在Rt△ADE中，∠AED=90°，BD=210m，∠D=30°，
解可得DE=105
．故选A．
点评：本题考查三角形的外角性质与勾股定理的应用．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
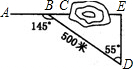如图，沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B，取∠ABD=145°，BD=500米，∠D=55度．要使A，C，E成一直线．那么开挖点E离点D的距离是（ ）| A、500sin55°米 | B、500cos55°米 | C、500tan55°米 | D、500cot55°米 |
如图，沿AC方向开山修路，为了预算的需要，设计人员打算测量CE之间的距离，设计图如图所示，△ABF∽△EBD，量得BD=500m，FB=100m，AB=80m，BC=80m，则CE的长为
如图，沿AC方向开山修渠，为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B取∠ABD=135°，BD=520m，∠D=45°，如果要使A，C，E成一直线，求开挖点E离D的距离（精确到1m）．
（2012•吉林）如图，沿AC方向开山修一条公路，为了加快施工速度，要在小山的另一边寻找点E同时施工．从AC上的一点B取∠ABD=127°，沿BD的方向前进，取∠BDE=37°，测得BD=520m，并且AC，BD和DE在同一平面内．
如图，沿AC方向开山修路，为了加快施工进度，要在山的另一面同时施工，工人师傅在AC上取一点B，在小山外取一点D，连接BD并延长，使DF=BD，过F点作AB的平行线MF，连接MD并延长，在延长线上取一点E，使DE=DM，在E点开工就能使A，C，E成一条直线，你知道其中的道理吗？