题目内容
如图在Rt△ABC中，∠C=90°，a、b分别是∠A，∠B的对边，如果sinA：sinB=2：3，那么a：b等于（ ）
| A．2：3 | B．3：2 | C．4：9 | D．9：4 |
设∠C所对的边为c，
∵Rt△ABC中，∠C=90°，
∴sinA=
，sinB=
，
∵sinA：sinB=2：3，
∴
=
=
，即a：b=2；3．
故选A．
∵Rt△ABC中，∠C=90°，
∴sinA=
| a |
| c |
| b |
| c |
∵sinA：sinB=2：3，
∴
| sinA |
| sinB |
| 2 |
| 3 |
| ||
|
故选A．
练习册系列答案
习题精选系列答案
相关题目
中，过点A分别作AE⊥BC于点E，AF⊥CD于点F．
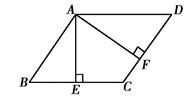
∠BAE=∠DAF；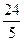
，
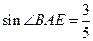，求CF的长．
