Question

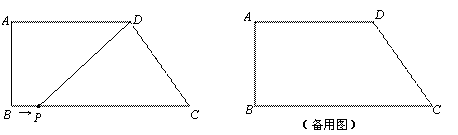
如图，直角梯形ABCD，AD∥BC，∠B＝90º，AD＝6，AB＝4，
BC＝9．

（1）CD的长为        ．

（2）点P从点B出发，以每秒1个单位的速度沿着边BC向点C运动，连接DP．设点P运动的时间为t秒，则当t为何值时，△PDC为等腰三角形？

（3）在（2）的条件下，点Q同时从点B出发，以每秒4个单位的速度沿着边BA、AD向点D运动，当点Q到达终点时两点同时停止运动．是否存在某一时刻t，使得以点P、Q、D、C为顶点的四边形是平行四边形？若存在，请求出t的值；若不存在，请说明理由．

 

Answer 1

   （2）过点D作DE⊥BC，垂足为E，由题意得PC＝9—t，PE＝6—t．

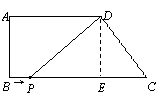        当CD＝CP时，5＝9—t，解得t＝4；

        当CD＝PD时，E为PC中点，

∴6—t＝3，∴t＝3；

        当PD＝PC时，PD²＝PC²，

∴(6—t)²＋4²＝(9—t)²，解得t＝．

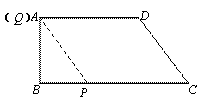（3）显然，当点Q在AB上时，以点P、Q、D、C为顶点的四边形不可能是平行四边形；          

  当点Q在AD上时，1≤t＜．

若四边形PQDC为平行四边形，则PC＝DQ．

  ∴9—t＝10—4t，解得t＝   （不合题意，舍去）．

  ∴不存在某一时刻t，使得以点P、Q、D、C为顶点的四边形是平行四边形．（7分）

       当3≤v＜时，在整个运动过程中，始终存在某一时刻，使四边形PQDC为平行四边形．