题目内容
如图，已知
，∠BAD=30°，则∠CAE=________°．
30
分析：由三边对应成比例的两个三角形相似可得△ABC∽△ADE，根据相似三角形的对应角相等得到所以∠BAC=∠DAE，进而得到∠BAD=∠CAE，再由两边对应成比例且夹角相等得到△BAD∽△CAE，根据相似三角形的对应角相等即可得出∠BAD=∠CAE的关系．
解答：
解：连接EC，
∵AB：AD=BC：DE=AC：AE，
∴△ABC∽△ADE．
∴∠BAC=∠DAE，∠BAD=∠CAE，
又∵AB：AD=AC：AE，∠BAD=∠CAE，
∴△BAD∽△CAE，
∴∠BAD=∠CAE，
∵∠BAD=30°，
∴∠CAE=30°，
故答案为：30．
点评：此题主要考查了相似三角形的判定定理及性质，关键是证明△BAD∽△CAE，根据相似三角形对应角相等可得答案．
分析：由三边对应成比例的两个三角形相似可得△ABC∽△ADE，根据相似三角形的对应角相等得到所以∠BAC=∠DAE，进而得到∠BAD=∠CAE，再由两边对应成比例且夹角相等得到△BAD∽△CAE，根据相似三角形的对应角相等即可得出∠BAD=∠CAE的关系．
解答：
解：连接EC，∵AB：AD=BC：DE=AC：AE，
∴△ABC∽△ADE．
∴∠BAC=∠DAE，∠BAD=∠CAE，
又∵AB：AD=AC：AE，∠BAD=∠CAE，
∴△BAD∽△CAE，
∴∠BAD=∠CAE，
∵∠BAD=30°，
∴∠CAE=30°，
故答案为：30．
点评：此题主要考查了相似三角形的判定定理及性质，关键是证明△BAD∽△CAE，根据相似三角形对应角相等可得答案．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
1、如图，已知△ABC≌△BAD，A和B，C和D分别是对应顶点．如果AB=6cm，BD=7cm，AD=4cm，那么BC的长为（ ）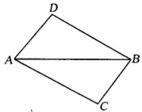
17、如图，已知△ABC≌△BAD，A和B、C和D是对应顶点．如果AB=6，BD=5，AD=4，那么BC的长度是
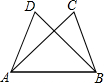如图，已知△ABC≌△BAD，AB=6cm，BD=7cm，AD=5cm，则BC的长等于（ ）
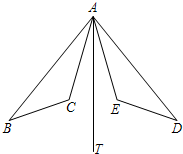如图，已知：∠BAD与∠CAE的平分线都是AT，AC=AE，∠B=∠D．
如图，已知，∠BAD=120°，AC平分∠BAD，若∠ABC+∠ADC=180°，则如下结论一定正确的有（ ）个