题目内容
如图,已知∠C=90°,四边形CDEF是正方形,AC=15,BC=10,AF与ED交于点G.则EG的长为 ( )
A. | B. | C. | D. |
D
由四边形CDEF是正方形,易证得△BEF∽△BAC,△EFG∽△DAG,EF=FC=CD=DE,然后设EF=x,则BF=BC-CF=10-x,利用相似三角形的对应边成比例,即可得方程,解此方程即可求得正方形CDEF的边长,继而求得AD的长,继而求得答案.
解:∵四边形CDEF是正方形,
∴EF=FC=CD=DE,EF∥CD,
设EF=x,则BF=BC-CF=10-x,
∴△BEF∽△BAC,
∴ =
= ,
,
∵AC=15,BC=10,
∴ =
= ,
,
解得:x=6,
∴EF=ED=CD=FC=6,
∴AD=AC-CD=15-6=9,
∵△EFG∽△DAG,
∴ =
= =
= ,
,
∴EG= ED=
ED= ×6=
×6= .
.
故选D.
此题考查了相似三角形的判定与性质与正方形的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用是解此题的关键.
解:∵四边形CDEF是正方形,
∴EF=FC=CD=DE,EF∥CD,
设EF=x,则BF=BC-CF=10-x,
∴△BEF∽△BAC,
∴
 =
= ,
,∵AC=15,BC=10,
∴
 =
= ,
,解得:x=6,
∴EF=ED=CD=FC=6,
∴AD=AC-CD=15-6=9,
∵△EFG∽△DAG,
∴
 =
= =
= ,
,∴EG=
 ED=
ED= ×6=
×6= .
.故选D.
此题考查了相似三角形的判定与性质与正方形的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用是解此题的关键.

练习册系列答案
相关题目




 中,
中, 两点在边
两点在边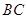 上,且四边形
上,且四边形 是平行四边形.
是平行四边形. 与
与 时,求证:
时,求证: 是矩形.
是矩形.


 是平行四边形
是平行四边形 对角线
对角线 上两点,
上两点, ,求证:
,求证: .
.