题目内容
 已知:如图所示,正方形ABCD和正方形AEFG有一个公共点A,连接BE、DG.线段BE、DG有怎样的关系?请证明你的结论.
已知:如图所示,正方形ABCD和正方形AEFG有一个公共点A,连接BE、DG.线段BE、DG有怎样的关系?请证明你的结论.
 证明:∵四边形ABCD和四边形AEFG都是正方形,
证明:∵四边形ABCD和四边形AEFG都是正方形,∴AB=AD,∠DAB=90°,AE=AF,∠EAG=90°,
∵∠EAB=∠DAB+∠EAD,∠GAD=∠EAG+∠EAD,
∴∠EAB=∠GAD,
在△EAB和△GAD中,
 ,
,∴△EAB≌△GAD(SAS),
∴BE=DG,∠EBA=∠GDA,
延长BE,交DG与点H,连结BD,
∵∠DAB=90°,
∴∠ADB+∠ABD=90°,
∴∠ADB+(∠DBE+∠EBA)=90°,
∴∠ADB+(∠DBE+∠GDA)=90°,
∴∠DHB=90°,
∴BE⊥DG.
分析:根据正方形的性质可得AB=AD,∠DAB=90°,AE=AF,∠EAG=90°,然后求出∠EAB=∠GAD,再利用“边角边”证明△EAB和△GAD全等,根据全等三角形对应边相等可得BE=DG,根据全等三角形对应角相等可得∠EBA=∠GDA,延长BE,交DG与点H,连结BD,然后求出∠DHB=90°,根据垂直的定义即可得证.
点评:本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并确定出全等的三角形然后找出全等的条件是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?
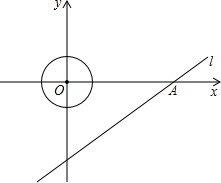
.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间? 已知:如图所示,直线l的解析式为
已知:如图所示,直线l的解析式为 ,并且与x轴、y轴分别交于点A、B.
,并且与x轴、y轴分别交于点A、B.
 x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.
 x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.