题目内容
如图所示，矩形ABCD的周长为20厘米，两条对角线相交于点O，过点O作AC的垂线EF，分别交AD、BC于E、F点，连接CE，则△CDE的周长为________．
10
分析：根据矩形的性质，AO=CO，由EF⊥AC，得EA=EC，则△CDE的周长是矩形周长的一半．
解答：∵AO=CO，EF⊥AC，
∴EF是AC的垂直平分线，
∴EA=EC，
∴△CDE的周长=CD+DE+CE=CD+AD=
矩形ABCD的周长=10．
故答案为10．
点评：本题考查了矩形的对角线互相平分的性质，还考查了线段垂直平分线的性质．
分析：根据矩形的性质，AO=CO，由EF⊥AC，得EA=EC，则△CDE的周长是矩形周长的一半．
解答：∵AO=CO，EF⊥AC，
∴EF是AC的垂直平分线，
∴EA=EC，
∴△CDE的周长=CD+DE+CE=CD+AD=
矩形ABCD的周长=10．故答案为10．
点评：本题考查了矩形的对角线互相平分的性质，还考查了线段垂直平分线的性质．
练习册系列答案
相关题目
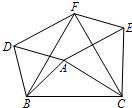18、如图所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE、等边△BCF．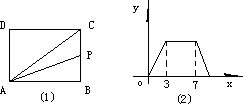
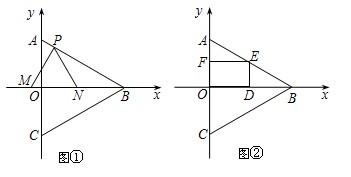
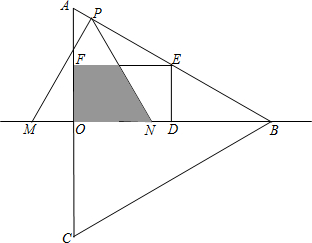边在△AOB内部作如图所示的矩形ODEF，点E在线段AB上．
（2012•邵阳）如图所示，在△ABC中，AB=AC，∠A＜90°，边BC、CA、AB的中点分别是D、E、F，则四边形AFDE是（ ）