题目内容
某初中要调查学校学生(总数 1000 人)双休日课外阅读情况,随机调查了一部分学生,调查得 到的数据分别制成频数直方图(如图 1)和扇形统计图(如图 2).

(1)请补全上述统计图(直接填在图中); 试确定这个样本的中位数和众数;
(3)请估计该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数.
【考点】条形统计图;用样本估计总体;扇形统计图;中位数;众数.
【分析】(1)根据阅读 5 小时以上频数为 6,所占百分比为 12%,求出数据总数,再用数据总数减 去其余各组频数得到阅读 3 小时以上频数,进而补全频数分布直方图,分别求得阅读 0 小时和 4 小 时的人数所占百分比,补全扇形图;
利用各组频数和总数之间的关系确定中位数和众数;
(3)用 1000 乘以每周课外阅读时间不小于 4 小时的学生所占百分比即可.
【解答】解:(1)总人数:6÷12%=50(人),
阅读 3 小时以上人数:50﹣4﹣6﹣8﹣14﹣6=12(人), 阅读 3 小时以上人数的百分比为 12÷50=24%,
阅读 0 小时以上人数的百分比为 4÷50=8%. 图如下:

中位数是 3 小时,众数是 4 小时;
(3)1000×
=1000×40%
=400(人)
答 :该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数为 400 人.
:该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数为 400 人.
【点评】此题主要考查了频数分布直方图、扇形统计图的能力和利用统计图获取信息的能力;利用 统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查 了利用样本估计总体.

练习册系列答案
相关题目





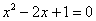 B、
B、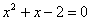
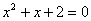 D、
D、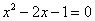
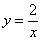 的图象的两个分支分别在( )
的图象的两个分支分别在( )