Question

已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F．

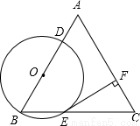
（1）求证：直线EF是⊙O的切线；

（2）当直线DF与⊙O相切时，求：⊙O的半径．

Answer 1

（1）证明见解析；（2）.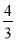

【解析】

试题分析：（1）连接OE．欲证直线EF是⊙O的切线，只需证明EF⊥AC．利用等边三角形的三个内角都是60°、等腰三角形OBE以及三角形的内角和定理求得同位角∠BOE=∠A=60°，从而判定OE∥AC，所以由已知条件EF⊥AC判定OE⊥EF，即直线EF是⊙O的切线；

（2）连接DF．设⊙O的半径是r．由等边三角形的三个内角都是60°、三条边都相等、以及在直角三角形中30°所对的直角边是斜边的一半求得关于r的方程4-r=2（4r-4），解方程即可．

试题解析：（1）证明：连接OE．

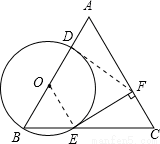
∵△ABC是等边三角形，

∴∠A=∠B=∠C=60°；

在△BOE中，OB=OE，∠B=60°，

∴∠B=∠OEB=∠BOE=60°，

∴∠BOE=∠A=60°，

∴OE∥AC；

∵EF⊥AC，

∴OE⊥EF，即直线EF是⊙O的切线；

（2）【解析】
连接DF．

∵DF与⊙O相切，

∴∠ADF=90°．

设⊙O的半径是r，则EB=r，EC=4-r，AD=4-2r．

在Rt△ADF中，∠A=60°，

∴AF=2AD=8-4r．

∴FC=4r-4；

在Rt△CEF中，∵∠C=60°，∴EC=2FC，

∴4-r=2（4r-4），

解得，r=；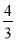

∴⊙O的半径是．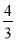

考点：1.切线的判定与性质；2.等边三角形的判定与性质．