题目内容
甲、乙两车同时同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程 (千米)与行驶时间
(千米)与行驶时间 (时)的函数图象如图所示.
(时)的函数图象如图所示.

(1)求甲车距离A地的路程 (千米)与行驶时间
(千米)与行驶时间 (时)之间的函数关系式;
(时)之间的函数关系式;
(2)当x=2.8时,甲、乙两车之间的距离是 千米;乙车到达B地所用的时间 的值为 ;
的值为 ;
(3)行驶过程中,两车出发多长时间首次后相遇?
【答案】
(1) ;(2)68,5.4;(3)4.5小时
;(2)68,5.4;(3)4.5小时
【解析】
试题分析:(1)由题意设函数关系式为 ,根据待定系数法即可求得结果;
,根据待定系数法即可求得结果;
(2)把x=2.8代入(1)中的函数关系式即可得到甲车的路程,从而得到甲、乙两车之间的距离;先求出乙车开始的行驶速度,即可得到修好后乙车的行驶速度,从而得到a的值;
(3)设修好后乙车距离A地的路程 (千米)与行驶时间
(千米)与行驶时间 (时)的函数关系式为
(时)的函数关系式为 ,根据待定系数法求得函数关系式后,再与(1)中的函数关系式组成方程组求解即可.
,根据待定系数法求得函数关系式后,再与(1)中的函数关系式组成方程组求解即可.
(1)设函数关系式为
∵图象过点(6,360)
∴ ,
,
∴甲车距离A地的路程 (千米)与行驶时间
(千米)与行驶时间 (时)之间的函数关系式为
(时)之间的函数关系式为 ;
;
(2)在 中,当x=2.8时,
中,当x=2.8时, 千米;
千米;
则甲、乙两车之间的距离
由图可得乙车开始的行驶速度为 千米/时
千米/时
则修好后乙车的行驶速度为 千米/时
千米/时
所以 ;
;
(3)设修好后乙车距离A地的路程 (千米)与行驶时间
(千米)与行驶时间 (时)的函数关系式为
(时)的函数关系式为
∵图象过点(2.8,100),(5.4,360)
∴ ,解得
,解得
∴函数关系式为
由题意得 ,解得
,解得
答:行驶过程中,两车出发4.5小时时间首次后相遇.
考点:一次函数的应用
点评:一次函数是常用的解答实际问题的数学模型,本题即是利用一次函数的有关知识解答实际应用题,是中考的常见题型.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
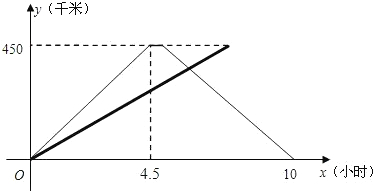
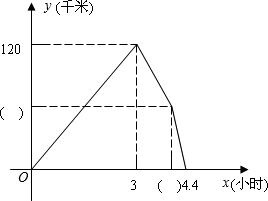
 (2013•锦州)甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
(2013•锦州)甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.