��Ŀ����
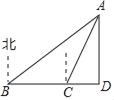
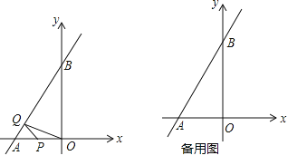
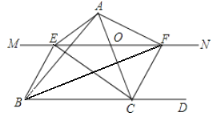
����Ŀ����ͼ����![]() �У���
����![]() ��
��![]() ����һ�����㣬����
����һ�����㣬����![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() ��ƽ�����ڵ�
��ƽ�����ڵ�![]() ����
����![]() �����
�����![]() ��ƽ�����ڵ�
��ƽ�����ڵ�![]() ��
��
��1��̽��![]() ��
��![]() ��������ϵ������֤��.
��������ϵ������֤��.
��2������![]() ������
������![]() �ڱ�
�ڱ�![]() ���˶�ʱ���ı���
���˶�ʱ���ı���![]() ����Ϊ�����������ܣ���֤�����������ܣ���˵�����ɣ�
����Ϊ�����������ܣ���֤�����������ܣ���˵�����ɣ�
��3������![]() ������
������![]() ��
��![]() ���˶���ʲôλ��ʱ���ı���
���˶���ʲôλ��ʱ���ı���![]() �Ǿ��Σ���˵�����ɣ�
�Ǿ��Σ���˵�����ɣ�
��4���ڣ�3���������£�![]() ����ʲô����ʱ���ı���
����ʲô����ʱ���ı���![]() �������Σ���˵��������
�������Σ���˵��������
���𰸡���1��![]() ��֤������������2���ı���
��֤������������2���ı���![]() ������Ϊ���Σ����ɼ���������3������
������Ϊ���Σ����ɼ���������3������![]() �˶���
�˶���![]() ���е�ʱ���ı���
���е�ʱ���ı���![]() �Ǿ��Σ����ɼ���������4������
�Ǿ��Σ����ɼ���������4������![]() �˶���
�˶���![]() ���е�ʱ����
���е�ʱ����![]() ����
����![]() Ϊֱ�ǵ�ֱ��������ʱ���ı���
Ϊֱ�ǵ�ֱ��������ʱ���ı���![]() �������Σ����ɼ�������
�������Σ����ɼ�������
��������
��1������![]() �ɵ�
�ɵ�![]() ���ٸ���
���ٸ���![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() �ǵõó��𰸣�
�ǵõó��𰸣�
��2������![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() �ɵá�ECF�Ķ������ٸ������ε����ʼ��ɵó����ۣ�
�ɵá�ECF�Ķ������ٸ������ε����ʼ��ɵó����ۣ�
��3����֤�ı���![]() ��ƽ���ı��Σ��̶���֤���Ǿ��Σ�
��ƽ���ı��Σ��̶���֤���Ǿ��Σ�
��4����ϣ�3�����ٸ���![]() ����
����![]() ���ɵó�����.
���ɵó�����.
�⣺��1��![]() ��
��
֤������![]() ��
��
��![]() ��
��
�֡�![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��2���ı���![]() ������Ϊ���Σ�
����������
���ɣ���![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
��![]() ��
��
���ı���![]() �����Σ���
��������![]() ����
����![]() �У������ܴ���������Ϊ90�㣬
�У������ܴ���������Ϊ90�㣬
���ı���BCFE������Ϊ���Σ�
��3������![]() �˶���
�˶���![]() ���е�ʱ���ı���
���е�ʱ���ı���![]() �Ǿ���.���ɣ�
�Ǿ���.���ɣ�
�ߵ���![]() �˶���
�˶���![]() ���е�ʱ��
���е�ʱ��![]() ��
��
�֡�![]() ��
��
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ���ı���
���ı���![]() �Ǿ���.
�Ǿ���.
��4������![]() �˶���
�˶���![]() ���е�ʱ����
���е�ʱ����![]() ����
����![]() Ϊֱ�ǵ�ֱ��������ʱ��
Ϊֱ�ǵ�ֱ��������ʱ��
�ı���![]() �����������ɣ�
�����������ɣ�
�ɣ�3��֪������![]() �˶���
�˶���![]() ���е�ʱ���ı���
���е�ʱ���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��֪![]() ����
����![]() ʱ��
ʱ��
![]() ��
��
��![]() ��
��
���ı���![]() �������Σ�
��������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�