Question

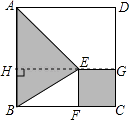
【题目】如图1，BA⊥MN，垂足为A，BA=4，点P是射线AN上的一个动点(不与点A重合)，∠BPC=∠BPA，BC⊥BP，过点C作CD⊥MN，垂足为D，设AP=x

（1）CD的长度是否随着x的变化而变化？若变化，用含x的代数式表示CD的长度；若不变化，求出线段CD的长度；
（2）△PBC的面积是否存在最小值？若存在，请求出这个最小值，并求出此时的x的值；若不存在，请说明理由；
（3）当x取何值时，△ABP和△CDP相似；
（4）如图2，当以C为圆心，以CP为半径的圆与线段AB有公共点时，求x的值。

Answer 1

【答案】
（1）解：CD的长度不变化，理由如下:
如图1,延长CB和PA,记交点为点Q.

, ,
(等腰三角形“三合一”的性质).
, ,
,
,

,
即CD=8 。
（2）解：如图2,过点B作 ,垂足为F.

, , . , ,即CP最小值为8, 面积的最小值
此时 是等腰三角形,AP=AB=4 ,即x=4;
（3）解：当 时,
,
,
即 ,
如图3,当

时,
, ,
,
,
,
即 ,
所以当 或 时, 和 相似。
（4）解：如图延长CB和PA相交于点E，

当点A在圆C上时，由（1）及垂径定理得
AE=AD=DP= x
由 得

∴
∴x的取值范围是
【解析】（1）CD的长度不变化，理由如下:如图1，延长CB和PA，记交点为点Q．根据等腰△QPC“三合一”的性质证得QB=BC；根据同一平面内垂直于同一直线的两条直线互相平行得出A B ∥ C D ,根据平行于三角形一边的直线截其它两边，所截得的三角形与原三角形相似得出：△QAB∽△QDC；由全等三角形的对应边成比例得出CD=2AB，从而得出答案；
（2）如图2，过点B作BF⊥PC，垂足为F．根据角平分线上的点到角两边的距离相等得出BF=BA=4．根据垂线段最短得出CP≥CD，从而得出CP最小值为8，根据三角形的面积公式进而得出△PBC面积的最小值，进而根据角平分线的定义得出此时△BAP是等腰直角三角形，AP=AB=4，进而得出答案；
（3）此题分两种情况 ：①当△BAP∽△CDP时，由∠ B P C = ∠ B P A , ∠ C P D = ∠ B P A 根据平角的定义得出∠BPA=60°，然后利用正切函数的定义得出x=AP=,②当Δ B A P Δ P D C 时,由∠ C P B = ∠ B P A , ∠ P C D = ∠ B P A ,根据直角三角形两锐角互余得出∠ B P A = 30 ,然后利用正切函数的定义得出x=AP= ；综上所述从而得出x的值；
（4）根据当点A在⊙C上时，由（1）及垂径定理得：AE=AD=DP=x,由全等三角形对应边成比例得出