ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯB=90 ЃЌAB=16cmЃЌBC=12cmЃЌPЁЂQЪЧЁїABCБпЩЯЕФСНИіЖЏЕуЃЌЦфжаЕуPДгЕуAПЊЪМбиAЁњBЗНЯђдЫЖЏЃЌЧвЫйЖШЮЊУПУы1cmЃЌЕуQДгЕуBПЊЪМбиBЁњCЁњAЗНЯђдЫЖЏЃЌЧвЫйЖШЮЊУПУы2cmЃЌЫќУЧЭЌЪБГіЗЂЃЌЩшГіЗЂЕФЪБМфЮЊtУыЃЎ
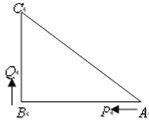
ЃЈ1ЃЉГіЗЂ2УыКѓЃЌЧѓPQЕФГЄЃЛ
ЃЈ2ЃЉЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂМИУыжгКѓЃЌЁїPQBФмаЮГЩЕШбќШ§НЧаЮЃП
ЃЈ3ЃЉЕБЕуQдкБпCAЩЯдЫЖЏЪБЃЌЧѓФмЪЙЁїBCQГЩЮЊЕШбќШ§НЧаЮЕФдЫЖЏЪБМфЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЕБtЮЊ11УыЛђ12УыЛђ13.2УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ
ЃЛЃЈ3ЃЉЕБtЮЊ11УыЛђ12УыЛђ13.2УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуPЁЂQЕФдЫЖЏЫйЖШЧѓГіAPЃЌдйЧѓГіBPКЭBQЃЌгУЙДЙЩЖЈРэЧѓЕУPQМДПЩЃЛ
ЃЈ2ЃЉЩшГіЗЂtУыжгКѓЃЌЁїPQBФмаЮГЩЕШбќШ§НЧаЮЃЌдђBP=BQЃЌгЩBQ=2tЃЌBP=8-tЃЌСаЪНЧѓЕУtМДПЩЃЛ
ЃЈ3ЃЉЕБЕуQдкБпCAЩЯдЫЖЏЪБЃЌФмЪЙЁїBCQГЩЮЊЕШбќШ§НЧаЮЕФдЫЖЏЪБМфгаШ§жжЧщПіЃКЂйЕБCQ=BQЪБЃЌдђЁЯC=ЁЯCBQЃЌПЩжЄУїЁЯA=ЁЯABQЃЌдђBQ=AQЃЌдђCQ=AQЃЌДгЖјЧѓЕУtЃЛЂкЕБCQ=BCЪБЃЌдђBC+CQ=24ЃЌвзЧѓЕУtЃЛЂлЕБBC=BQЪБЃЌЙ§BЕузїBEЁЭACгкЕуEЃЌдђЧѓГіBEЃЌCEЃЌМДПЩЕУГіtЃЎ
ЃЈ1ЃЉЕБt=2ЪБBQ=2ЁС2=4 cmЃЌBP=AB-AP=16-2ЁС1=14 cm ЃЌЁЯB=90ЁуЃЌ
ЁрPQ=![]() =
=![]() cm
cm
(2)вРЬтвтЕУЃК BQ=2t ЃЌBP=16-t
2t =16-t НтЕУЃКt=![]()
МДГіЗЂ![]() УыжгКѓЃЌЁїPQBФмаЮГЩЕШбќШ§НЧаЮЃЛ
УыжгКѓЃЌЁїPQBФмаЮГЩЕШбќШ§НЧаЮЃЛ
(3) ЂйЕБCQ=BQЪБ(ШчЯТЭМ)ЃЌдђЁЯC=ЁЯCBQЃЌ

ЁпЁЯABC=90Ёу
ЁрЁЯCBQ+ЁЯABQ=90Ёу
ЁЯA+ЁЯC=90Ёу
ЁрЁЯA=ЁЯABQ
ЁрBQ=AQ
ЁрCQ=AQ=10
ЁрBC+CQ=22
Ёрt=22ЁТ2=11Уы
ЂкЕБCQ=BCЪБЃЈШчЭМ2ЃЉЃЌдђBC+CQ=24
Ёрt=24ЁТ2=12Уы
ЂлЕБBC=BQЪБЃЈШчЭМ3ЃЉЃЌЙ§BЕузїBEЁЭACгкЕуEЃЌ

дђBE=![]() ЃЌ
ЃЌ
ЁрCE=![]() ЃЌ
ЃЌ
ЙЪCQ=2CE=14.4,
ЫљвдBC+CQ=26.4ЃЌ
Ёрt=26.4ЁТ2=13.2Уы
гЩЩЯПЩжЊЃЌЕБtЮЊ11УыЛђ12УыЛђ13.2УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ