题目内容
若抛物线y=(a+1)x2-(a+1)x+1与x轴有且仅有一个公共点,则a的值为 .
考点:抛物线与x轴的交点
专题:
分析:根据y=(a+1)x2-(a+1)x+1与x轴有且仅有一个公共点,则b2-4ac=(a+1)2-4(a+1)=a2-2a-3=0,进而得出即可.
解答:解:∵y=(a+1)x2-(a+1)x+1与x轴有且仅有一个公共点,
∴b2-4ac=(a+1)2-4(a+1)=a2-2a-3=0,
解得:a1=3,a2=-1,当a=-1,则a+1=0,故舍去.
故答案为:3.
∴b2-4ac=(a+1)2-4(a+1)=a2-2a-3=0,
解得:a1=3,a2=-1,当a=-1,则a+1=0,故舍去.
故答案为:3.
点评:此题主要考查了抛物线与x轴的交点,根据题意得出b2-4ac=0得出是解题关键.

练习册系列答案
相关题目
从1~12这十二个自然数中任取一个,取到的数恰好是4的倍数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,△ABC中,∠ACB=90°,AC=3,BC=4.以A为圆心作圆与BC相切,则该圆的半径为( )
如图,△ABC中,∠ACB=90°,AC=3,BC=4.以A为圆心作圆与BC相切,则该圆的半径为( )| A、2.5 | B、3 | C、4 | D、5 |
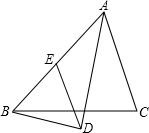 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长. 如图,在一个正方体的两个面上画了两条对角线AB,AC,那么∠CAB的值是
如图,在一个正方体的两个面上画了两条对角线AB,AC,那么∠CAB的值是