题目内容
已知抛物线y=x2+bx+c(其中b>0,c≠0)与y轴的交点为A,点A关于抛物线对称轴的对称点为B(m,n),且AB=2.(1)求m、b的值;
(2)如果抛物线的顶点位于x轴的下方,且BO=
| 20 |
分析:(1)由抛物线y=x2+bx+c(其中b>0,c≠0)与y轴的交点为A,即可求得点A的坐标,又由点A关于抛物线对称轴的对称点为B(m,n),且AB=2,即可得抛物线的对称轴方程,又由抛物线y=x2+bx+c的对称轴方程为x=-
与b>0,即可求得b与M的值;
(2)由(1)可得:A(0,c),B(-2,c),然后分别从若A在x轴下方与若A在x轴上方去分析,根据勾股定理即可求得c的值,注意抛物线的顶点位于x轴的下方.
| b |
| 2 |
(2)由(1)可得:A(0,c),B(-2,c),然后分别从若A在x轴下方与若A在x轴上方去分析,根据勾股定理即可求得c的值,注意抛物线的顶点位于x轴的下方.
解答: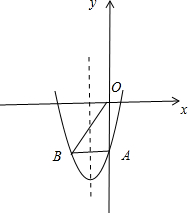 解:(1)∵抛物线y=x2+bx+c(其中b>0,c≠0)与y轴的交点为A,
解:(1)∵抛物线y=x2+bx+c(其中b>0,c≠0)与y轴的交点为A,
∴点A的坐标为(0,c),
∵点A关于抛物线对称轴的对称点为B(m,n),且AB=2,
∴抛物线y=x2+bx+c的对称轴方程为:x=±1,
∵抛物线y=x2+bx+c的对称轴方程为x=-
,
∵b>0,
∴抛物线y=x2+bx+c的对称轴方程为x=-1,
∴b=2,m=-2;
(2)如图:①若A在x轴下方,可得:A(0,c),B(-2,c),
∵BO=
,AB=2,
∴OA=
=4,
∴c=-4,
∴抛物线所对应的函数关系式为:y=x2+2x-4,
②若A在x轴上方,同理可得:c=4,
即抛物线所对应的函数关系式为:y=x2+2x+4,
此时顶点坐标为(-1,3),
∵抛物线的顶点位于x轴的下方,
∴舍去;
∴抛物线所对应的函数关系式为:y=x2+2x-4.
 解:(1)∵抛物线y=x2+bx+c(其中b>0,c≠0)与y轴的交点为A,
解:(1)∵抛物线y=x2+bx+c(其中b>0,c≠0)与y轴的交点为A,∴点A的坐标为(0,c),
∵点A关于抛物线对称轴的对称点为B(m,n),且AB=2,
∴抛物线y=x2+bx+c的对称轴方程为:x=±1,
∵抛物线y=x2+bx+c的对称轴方程为x=-
| b |
| 2 |
∵b>0,
∴抛物线y=x2+bx+c的对称轴方程为x=-1,
∴b=2,m=-2;
(2)如图:①若A在x轴下方,可得:A(0,c),B(-2,c),
∵BO=
| 20 |
∴OA=
| OB2-AB2 |
∴c=-4,
∴抛物线所对应的函数关系式为:y=x2+2x-4,
②若A在x轴上方,同理可得:c=4,
即抛物线所对应的函数关系式为:y=x2+2x+4,
此时顶点坐标为(-1,3),
∵抛物线的顶点位于x轴的下方,
∴舍去;
∴抛物线所对应的函数关系式为:y=x2+2x-4.
点评:此题考查了二次函数的综合应用.此题难度较大,解题的关键是掌握二次函数的对称性,注意勾股定理的应用,注意数形结合思想的应用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.