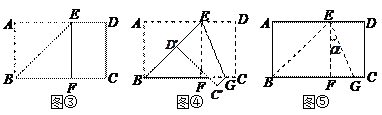题目内容
在△ABC中,BE平分∠ABC交AC于点E,ED∥CB交AB于点D,已知:AD=1,DE=2,则BC的长为
- A.3
- B.4
- C.5
- D.6
D
分析:因为ED∥CB,所以∠1=∠3,又因为BE平分∠ABC,所以∠1=∠2.故∠2=∠3,根据等角对等边,BD=DE=2,根据平行线分线段成比例定理, =
= ,即
,即 =
= ,解得BC=6.
,解得BC=6.
解答: 解:∵ED∥CB,
解:∵ED∥CB,
∴∠1=∠3,
又∵BE平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BD=DE=2,
又∵ED∥CB,
∴ =
= ,
,
∵AD=1,DE=2,
∴AB=AD+BD=AD+DE=3,
即 =
= ,
,
∴BC=6.
故选D.
点评:此题结合了平行线的性质和平行线分线段成比例定理,构思巧妙,是一道很好的题.
分析:因为ED∥CB,所以∠1=∠3,又因为BE平分∠ABC,所以∠1=∠2.故∠2=∠3,根据等角对等边,BD=DE=2,根据平行线分线段成比例定理,
 =
= ,即
,即 =
= ,解得BC=6.
,解得BC=6.解答:
 解:∵ED∥CB,
解:∵ED∥CB,∴∠1=∠3,
又∵BE平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BD=DE=2,
又∵ED∥CB,
∴
 =
= ,
,∵AD=1,DE=2,
∴AB=AD+BD=AD+DE=3,
即
 =
= ,
,∴BC=6.
故选D.
点评:此题结合了平行线的性质和平行线分线段成比例定理,构思巧妙,是一道很好的题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

 (2013•平南县二模)如图,在扇形EAB中,半径长AB=10,∠EAB=90°;以AB为直径作半圆O,点D是弧BE上的一个动点,BD与半圆O交于点C,DG⊥AB于点G,DG与AC交于点F,连结OF.
(2013•平南县二模)如图,在扇形EAB中,半径长AB=10,∠EAB=90°;以AB为直径作半圆O,点D是弧BE上的一个动点,BD与半圆O交于点C,DG⊥AB于点G,DG与AC交于点F,连结OF.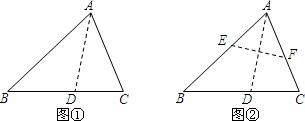 猜想、探究题:
猜想、探究题: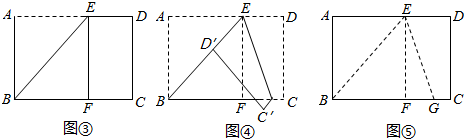

 处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠
处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠ 的大小是多少?(直接回答,不用说明理由).
的大小是多少?(直接回答,不用说明理由).

 处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠
处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠ 的大小是多少?(直接回答,不用说明理由).
的大小是多少?(直接回答,不用说明理由).