Question

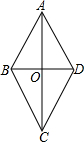如图所示，菱形ABCD的对角线AC=4+2

3

，BD=4-2

3

时，求菱形的边长和面积．

Answer 1

分析：根据菱形的对角线互相垂直平分求出OA、OB，再利用勾股定理列式计算即可求出边长AB，根据菱形的面积等于对角线乘积的一半列式计算即可．

解答：解：在菱形ABCD中，AC⊥BD，
OA=

1

2

AC=

1

2

（4+2

3

）=2+

3

，
OB=

1

2

BD=

1

2

（4-2

3

）=2-

3

，
根据勾股定理，AB=

OA2+OB2

=

(2+ 3 )2+(2- 3 )2

=

14

；

面积为：

1

2

×（4+2

3

）×（4-2

3

）=

1

2

×（16-12）=2．

点评：本题考查了二次根式的应用，菱形的对角线互相垂直平分的性质以及菱形的面积等于对角线乘积的一半的求法．