题目内容
如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.

证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△ABF和△AEC中,
∵ ,
,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)如图,根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°,
所以EC⊥BF.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

|
| A. | BC=B′C′ | B. | ∠A=∠A′ | C. | AC=A′C′ | D. | ∠C=∠C′ |

 ,AD⊥BC,垂足为D,如果CD=1,AD=2,BD=4
,AD⊥BC,垂足为D,如果CD=1,AD=2,BD=4

 -2=_______;
-2=_______; )-(-2
)-(-2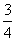 )-(-1
)-(-1 )×(3
)×(3 )×
)× ×
× .
.