题目内容
已知四边形的四条边的长分别是m、n、p、q，且满足m2+n2+p2+q2=2mn+2pq．则这个四边形是
- A.平行四边形
- B.对角线互相垂直的四边形
- C.平行四边形或对角线互相垂直的四边形
- D.对角线相等的四边形
C
分析：对于所给等式m2+n2+p2+q2=2mn+2pq，先移项，故可配成两个完全式，即（m-n）2+（p-q）2=0，进而可得m=n，p=q，四边形中两组邻边相等，故可判定是平行四边形或对角线互相垂直的四边形．
解答：m2+n2+p2+q2=2mn+2pq
可化简为（m-n）2+（p-q）2=0
∴m=n，p=q，
∵m，n，p，q分别为四边形的四边
∴m，n为对边，p=q为对边，
∴可确定其为平行四边形
当m，n为邻边时，可以证明有两个顶点在一条对角线的垂直平分线上，
∴四边形的对角线互相垂直的四边形．
故选B．
点评：此题主要考查平行四边形的判定问题，正确的对式子进行变形，熟练掌握平行四边形的判定定理是解题的关键．
分析：对于所给等式m2+n2+p2+q2=2mn+2pq，先移项，故可配成两个完全式，即（m-n）2+（p-q）2=0，进而可得m=n，p=q，四边形中两组邻边相等，故可判定是平行四边形或对角线互相垂直的四边形．
解答：m2+n2+p2+q2=2mn+2pq
可化简为（m-n）2+（p-q）2=0
∴m=n，p=q，
∵m，n，p，q分别为四边形的四边
∴m，n为对边，p=q为对边，
∴可确定其为平行四边形
当m，n为邻边时，可以证明有两个顶点在一条对角线的垂直平分线上，
∴四边形的对角线互相垂直的四边形．
故选B．
点评：此题主要考查平行四边形的判定问题，正确的对式子进行变形，熟练掌握平行四边形的判定定理是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
中，已知抛物线经过点Ａ(0，4)，B(1，0)，C（5，0），抛物线对称轴
与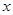
轴相交于点M．
）上的一点，若以A、O、M、P为顶点的四边形四条边的长度为四个连续的
和四边形
为例，分为以下四类：
，
，
，
，
；
；
，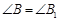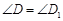