题目内容
设如图一系列图形中最外边的正方形边长都是1,依次连接正方形四边中点得新的正方形,观察图形,则第n个图形中所有三角形的面积是

- A.1-(
 )n
)n - B.1-(
 )n
)n - C.(
 )n
)n - D.(
 )n
)n
A
分析:根据正方形、三角形的面积公式和三角形中位线的性质分别求出第一个,第二个三角形的面积,从而找出规律,根据规律即可第n个图形中所有三角形的面积.
解答:∵第1个图形中所有三角形的面积是1×1- ×
× =1-(
=1-( )1,
)1,
第2个图形中所有三角形的面积是1×1- =1-(
=1-( )2,
)2,
第3个图形中所有三角形的面积是1×1- =1-(
=1-( )3,
)3,
…
∴第n个图形中所有三角形的面积是1-( )n;
)n;
故选A.
点评:此题考查了图形的变化类,解题的关键是通过观察、归纳与总结,得到其中的规律,大正方形的面积减去最中间小正方形的面积就是三角形的面积.
分析:根据正方形、三角形的面积公式和三角形中位线的性质分别求出第一个,第二个三角形的面积,从而找出规律,根据规律即可第n个图形中所有三角形的面积.
解答:∵第1个图形中所有三角形的面积是1×1-
 ×
× =1-(
=1-( )1,
)1,第2个图形中所有三角形的面积是1×1-
 =1-(
=1-( )2,
)2,第3个图形中所有三角形的面积是1×1-
 =1-(
=1-( )3,
)3,…
∴第n个图形中所有三角形的面积是1-(
 )n;
)n;故选A.
点评:此题考查了图形的变化类,解题的关键是通过观察、归纳与总结,得到其中的规律,大正方形的面积减去最中间小正方形的面积就是三角形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

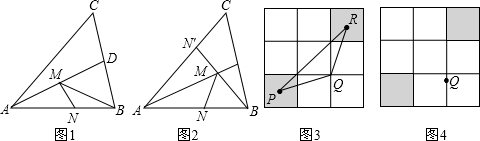
 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?

 )n
)n )n
)n )n
)n )n
)n