Question

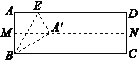
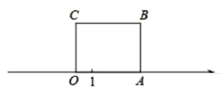
【题目】如图1，长方形的边在数轴上，为原点，长方形的面积为12，边的长为3

（1）数轴上点表示的数为

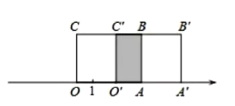
（2）将长方形沿数轴水平移动，移动后的长方形记为，设长方形移动的距离为，移动后的长方形与原长方形重叠部分的面积记为

①当等于原长方形面积的时，则点的移动距离 ，此时数轴上点表示的数为

②为线段的中点，点在线段上，且当点所表示的数互为相反数时，则的值为

Answer 1

【答案】（1）4；（2）①3；7；②

【解析】

（1）利用面积÷OC可得AO长，进而可得答案；

（2）①首先计算出S的值，再根据矩形的面积表示出O′A的长度，再分两种情况：当向左运动时，当向右运动时，分别求出A′表示的数；

②此题分两种情况：当原长方形OABC向左移动时，点D表示的数为4-x，点E表示的数为-x，再根据题意列出方程；当原长方形OABC向右移动时，点D，E表示的数都是正数，不符合题意．

（1）∵长方形OABC的面积为12，OC边长为3，

∴OA=12÷3=4，

∴数轴上点A表示的数为4，

故答案为：4．

（2）①∵S等于原长方形OABC面积的，

∴重叠部分的面积为3，即OA′×O′C′=3，

∵O′C′=3，

∴OA′=1，

则点A的移动距离AA′=3；

当向左运动时，如图1，A′表示的数为4-3=1，

当向右运动时，如图2，

∵O′A′=AO=4，

∴OA′=4+3=7，

∴A′表示的数为7，

故答案为：1或7．

②如图1，当原长方形OABC向左移动时，点D表示的数为4-x，点E表示的数为-x，

由题意可得方程：4-x-x=0，

解得：x=，

如图2，当原长方形OABC向右移动时，点D，E表示的数都是正数，不符合题意．

综上x的值为．