��Ŀ����
����Ŀ����ͼ��1����������ȫ�ȵ�ֱ�������Σ�ֱ�DZ߷ֱ�Ϊa��b��б��Ϊc����
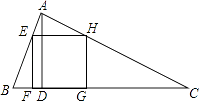
��1�������������������ι������ͼ��2����ͼ�Σ�B��E��C������һ��ֱ���ϣ����������ͼ�Σ���֤��![]() ��
��
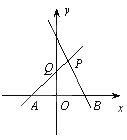
��2����a=1��b=2ʱ��������һ��ֱ�������η���ƽ��ֱ������ϵ�У���ͼ��3������ʹֱ�Ƕ�����ԭ���غϣ���ֱ�DZ�a��b�ֱ���x�ᡢy���غϣ���������������һ��C��ʹ��ABCΪ���������Σ�
��д��һ��������������x���ϵĵ�����꣺ ��
��д��һ��������������y���ϵĵ�����꣺ ��
��������������y���ϵĵ㹲�� ����

���𰸡���1������������2���ٴ𰸲�Ψһ���磺����1��0�����ڴ𰸲�Ψһ���磺��0��2+![]() ������4��
������4��
��������
��1����ͼ֪�����ε������������ֱ�������ε����֮��������ĸ��ʾ���������������֤�����ɶ�����
��2�����ݵ��������ε����ʷ������������������AΪԲ����ABΪ�뾶��Բ������BΪԲ����ABΪ�뾶��Բ������AB�Ĵ�ֱƽ������
��1����ͼ�ɵ���![]() ����a+b����a+b��=
����a+b����a+b��=![]() ab+
ab+![]() c2+
c2+![]() ab����������
ab����������![]() =
=![]() ����a2+2ab+b2=2ab+c2����a2+b2=c2��
����a2+2ab+b2=2ab+c2����a2+b2=c2��
��2����ͼ����һ��������������x���ϵĵ���������𰸲�Ψһ���磺����1��0����
��һ��������������y���ϵĵ���������𰸲�Ψһ���磺��0��2+![]() ����
����
��������������y���ϵĵ㹲�� 4����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�