题目内容
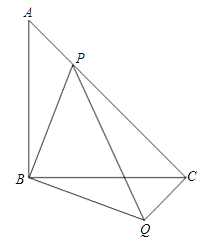
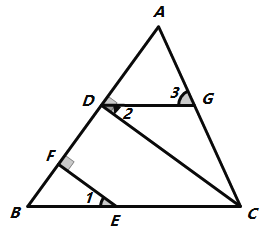
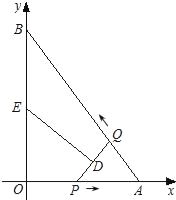
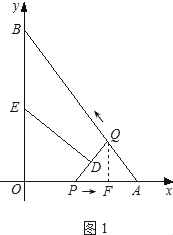
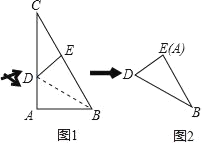
【题目】在三角形纸片ABC中，∠A＝90°，∠C＝30°，AC＝10cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），剪去△CDE后得到双层△BDE（如图2），再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为_____cm．
【答案】40或
．
【解析】
利用30°角直角三角形的性质，首先根据勾股定理求出DE的长，再分两种情形分别求解即可解决问题；
如图1中，
，
，
，
，
，设
，
在
中，
，
，
，
如图2中，当
时，沿着直线EF将双层三角形剪开，展开后的平面图形中有一个是平行四边形，此时周长
．
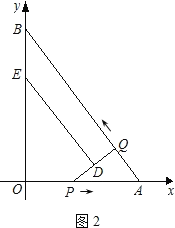
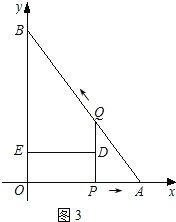
如图
中，当
时，沿着直线DF将双层三角形剪开，展开后的平面图形中有一个是平行四边形，此时周长
综上所述，满足条件的平行四边形的周长为
或
，
故答案为为
或
．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
