题目内容
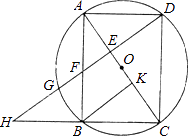
【题目】已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为K．过D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．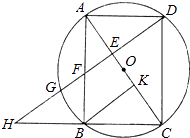 
（1）求证：AE=CK；
（2）如果AB=a，AD= 
（a为大于零的常数），求BK的长：
（3）若F是EG的中点，且DE=6，求⊙O的半径和GH的长．
【答案】
（1）证明：∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，
∴∠DAE=∠BCK，
∵BK⊥AC，DH∥KB，
∴∠BKC=∠AED=90°，
∴△BKC≌△ADE，
∴AE=CK
（2）解：∵AB=a，AD= 
=BC，
∴AC= 
= 
= 
∵BK⊥AC，∠ABC=90°，
∴在Rt△ABC中，由三角形的面积公式得： 
AB×BC= AC×BK，
∴a× 
a= 
a×BK，
∴BK= 
a
（3）解：DG是圆的弦，又有AE⊥GD得GE=ED，
∵DE=6，
∴GE=6，
又∵F为EG中点，
∴EF= EG=3，
∵△BKC≌△DEA，
∴BK=DE=6，
∴EF= BK，且EF∥BK，
∴△AEF∽△AKB，且相似比为1：2，
∴EF为△ABK的中位线，
∴AF=BF，
又∵∠ADF=∠H，∠DAF=∠HBF=90°，
∴△AFD≌△BFH（AAS），
∴HF=DF=3+6=9，
∴GH=6，
∵DH∥KB，BK⊥AC，四边形ABCD为矩形，
∴∠AEF=∠DEA=90°，
∴∠FAE+∠DAE=∠FAE+∠AFE=90°，
∴∠AFE=∠DAE，
∴△AEF∽△DEA，
∴AE：ED=EF：AE，
∴AE2=EFED=3×6=18，
∴AE=3 
，
∵△AED∽△HEC，
∴ 
= 
= ，
∴AE= AC，
∴AC=9 ，
则AO= 
，
故⊙O的半径是 ，GH的长是6．
【解析】（1）根据ABCD是矩形，求证△BKC≌△ADE即可；（2）根据勾股定理求得AC的长，根据三角形的面积公式得出 AB×BC= 
AC×BK，代入即可求得BK．（3）根据三角形中位线定理可求出EF，再利用△AFD≌△HBF可求出HF，然后即可求出GH；利用射影定理求出AE，再利△AED∽△HEC求证AE= AC，然后即可求得AC即可．
【考点精析】掌握三角形中位线定理和垂径定理是解答本题的根本，需要知道连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
