题目内容
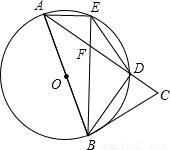
已知：如图，AB为圆O直径，C为圆O上一点，延长BC到D使CD＝BC，连结AD，作CE⊥AD，垂足为E，BE交圆O于F．
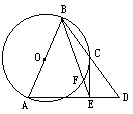
求证：
(1)CE是圆O的切线；
(2)EF·EB＝AE·DE．
答案：
解析：
解析：
|
证明：连结AC，
(1)因为AB为圆O的直径，所以AC⊥BD于C， 因为BC＝CD，所以AB＝AD，∠BAC＝∠DAC 连结OC，因为OA＝OC，所以∠BAC＝∠OCA，∠DAC＝∠OCA，OC∥AD． 因为CE⊥AD，所以CE⊥OC，CE是圆O切线，切点为C． (2)因为AC⊥CD，CE⊥AD，所以由射影定理 又由切割线定理， |
＝AE·DE
练习册系列答案
相关题目
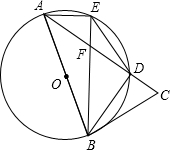E交AC于F，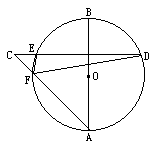
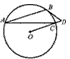
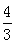，求CD的长。
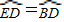，BE交AC于F，