Question

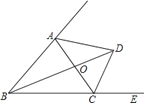
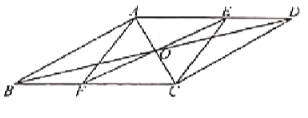
【题目】如图，在中，对角线，交于点，是上任意一点，连接并延长，交于点，连接，．

（1）求证：四边形是平行四边形；

（2）若，，．求出的边上的高的值．

Answer 1

【答案】(1)详见解析;(2)

【解析】

(1)根据平行四边形性质得BO=DO,AO=CO,AD∥BC,构造条件证△AOE≌△COF（ASA）,证CF=AE,CF∥AE,即可;

(2)作AH⊥BC,根据直角三角形性质得CH=,再运用勾股定理可得.

证明:（1）∵在ABCD中,AC,BD交于点O,
∴BO=DO,AO=CO,AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中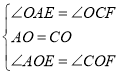
,
∴△AOE≌△COF（ASA）,
∴CF=AE,
∵CF∥AE,

∴四边形AFCE是平行四边形.

(2)作AH⊥BC,

因为四边形是平行四边形,

所以AD∥BC,

所以∠DAH=∠AHC=90°,

因为,

所以∠CAH=30°,

所以CH=

所以AH=

所以的边上的高的值是.