题目内容
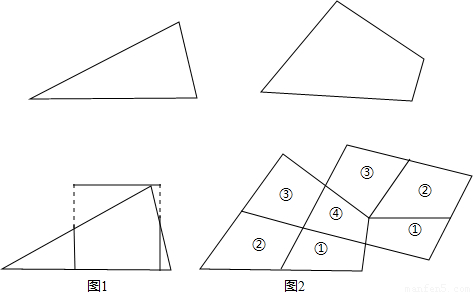
 小李同学设计了一个图案,图案是以斜边长为12cm的等腰直角三角形的各边为直径作半圆(如图所示),则图中阴影部分的面积为( )
小李同学设计了一个图案,图案是以斜边长为12cm的等腰直角三角形的各边为直径作半圆(如图所示),则图中阴影部分的面积为( )| A、36πcm2 | B、72πcm2 | C、36cm2 | D、72cm2 |
分析:阴影部分的面积等于中间等腰直角三角形的面积加上两个小半圆的面积,减去其中下面面积较大的半圆的面积.
解答:解:∵斜边长为12cm,则两直角边均为6
cm,
∴两个小半圆的面积均为:
π(3
)2=9πcm2,
以斜边为直径的半圆的面积是
π(
)2=18πcm2,
以斜边长为12cm的等腰直角三角形的面积是36cm2,
∴阴影部分的面积=9π+9π+36-18π=36cm2.
故选C.
| 2 |
∴两个小半圆的面积均为:
| 1 |
| 2 |
| 2 |
以斜边为直径的半圆的面积是
| 1 |
| 2 |
| 12 |
| 2 |
以斜边长为12cm的等腰直角三角形的面积是36cm2,
∴阴影部分的面积=9π+9π+36-18π=36cm2.
故选C.
点评:本题考查勾股定理的知识,将图形中不规则图形的面积转化为规则图形的面积的和或差是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目





 小李同学设计了一个图案,图案是以斜边长为12cm的等腰直角三角形的各边为直径作半圆(如图所示),则图中阴影部分的面积为
小李同学设计了一个图案,图案是以斜边长为12cm的等腰直角三角形的各边为直径作半圆(如图所示),则图中阴影部分的面积为