Question

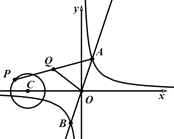
【题目】如图，一次函数y＝3x与反比例函数y＝(k＞0)的图象交于A，B两点，点P在以C(﹣3，0)为圆心，1为半径的⊙C上，Q是AP的中点，已知OQ长的最大值为2，则k的值为____.

Answer 1

【答案】

【解析】

连接BP，根据中位线定理可得BP长的最大值为，当BP过圆心C时，BP最长，过B作轴与D，设，则 即 根据勾股定理可得列出方程求出点B的坐标，代入反比例函数解析式即可求解.

连接BP，由对称性得：OA=OB,

Q是AP的中点，

OQ的长的最大值为2，则BP长的最大值为，

如图所示：

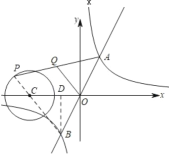
当BP过圆心C时，BP最长，过B作轴与D，

CP=1，，B在直线y＝3x上，

设，则 即

在 中，由勾股定理得：

解得：（舍去），或，

B在反比例函数y＝(k＞0)的图像上，

故答案为：