题目内容
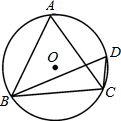如图，在⊙O中∠ACB=∠BDC=60°，
，则⊙O的周长是________．
4π
分析：根据圆周角定理，得∠A=∠BDC=60°，从而判断△ABC是等边三角形，再根据等边三角形的性质求得其外接圆的直径，从而求得其周长．
解答：
解：连接OC，作OE⊥AC于E．
∵∠ACB=∠BDC=60°，
∴∠A=∠BDC=60°，
∴△ABC是等边三角形，
∴∠OCE=30°，CE=
AC=
（垂径定理），
∴OC=
=2，
则⊙O的周长是4π．
故答案为4π．
点评：此题考查了圆周角定理、等边三角形的判定及性质．
注意：等边三角形的外心和内心重合，是它的三边垂直平分线的交点．
分析：根据圆周角定理，得∠A=∠BDC=60°，从而判断△ABC是等边三角形，再根据等边三角形的性质求得其外接圆的直径，从而求得其周长．
解答：
解：连接OC，作OE⊥AC于E．∵∠ACB=∠BDC=60°，
∴∠A=∠BDC=60°，
∴△ABC是等边三角形，
∴∠OCE=30°，CE=
AC=（垂径定理），∴OC=
=2，则⊙O的周长是4π．
故答案为4π．
点评：此题考查了圆周角定理、等边三角形的判定及性质．
注意：等边三角形的外心和内心重合，是它的三边垂直平分线的交点．
练习册系列答案
相关题目
如图，在△ABC中AC＞BC，E、D分别是AC、BC上的点，且∠BAD=∠ABE，AE=BD．
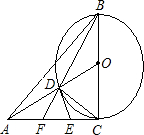如图，在△ABC中AC=BC，∠ACB=90°，以BC为直径作⊙O，连接OA，交⊙O于点D，过D点作⊙O的切线交AC于点E，连接B、D并延长交AC于点F．则下列结论错误的是（ ）| A、△ADE∽△ACO | B、△AOC∽△BFC | C、△DEF∽△DOC | D、CD2=DF•DB |
如图，在△ABC中AC=
如图，在△ABC中AC＞BC，E、D分别是AC、BC上的点，且∠BAD=∠ABE，AE=BD．