题目内容

已知:如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D.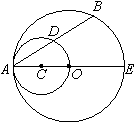

求证：点D是AB的中点.

连接OD，由OA为⊙C的直径可得∠ADO=90°，再根据垂径定理即可证得结论.

解析试题分析：连接OD

∵OA为⊙C的直径
∴∠ADO=90°
∴AD=BD
∴点D是AB的中点.
考点：圆周角定理，垂径定理
点评：解题的关键是熟练掌握垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧.

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

附加题：
已知：如图⊙O是以等腰三角形ABC的底边BC为直径的外接圆，BD平分∠ABC交⊙O于D，且BD与OA、

AC分别交于点E、F延长BA、CD交于G．
（1）试证明：BF=CG．
（2）线段CD与BF有什么数量关系？为什么？
（3）试比较线段CD与BE的大小关系，并说明理由．

22、已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF．
（1）求证：BE=DF；
（2）连接AC交EF于点O，延长OC至点G，使OG=OA，连接EG、FG．判断四边形AEGF是什么特殊四边形？并证明你的结论．

已知，如图，在平行四边形ABCD中，AC、BD相交于O点，点E、F分别为BO、DO的中点，试证明：
（1）OA=OC，OB=OD；
（2）四边形AECF是平行四边形；
（3）如果E、F点分别在DB和BD的延长线上时，且满足BE=DF，上述结论仍然成立吗？请说明理由．

已知：如图⊙O是以等腰三角形ABC的底边BC为直径的外接圆，BD平分∠ABC交⊙O于D，且BD与OA、
AC分别交于点E、F延长BA、CD交于G．
（1）试证明：BF=CG．
（2）线段CD与BF有什么数量关系？为什么？
（3）试比较线段CD与BE的大小关系，并说明理由．

附加题：
已知：如图⊙O是以等腰三角形ABC的底边BC为直径的外接圆，BD平分∠ABC交⊙O于D，且BD与OA、AC分别交于点E、F延长BA、CD交于G．
（1）试证明：BF=CG．
（2）线段CD与BF有什么数量关系？为什么？
（3）试比较线段CD与BE的大小关系，并说明理由．