题目内容
如图,正方形ABCO的边长为4,D为OC边的中点,将△DCB沿直线BD对折,C点落在M处,BM的延长线交OA于点E,OA,OC分别在x轴和y轴的正半轴上.
(1)求线段OE的长;
(2)求经过D,E两点,对称轴为直线x=2的抛物线的解析式;
(3)在抛物线的对称轴上是否存在点P,使四边形P、E、D、B为顶点的四边形是梯形?若存在,求出点P的坐标;若不存在,请说明理由.

1)解:∵四边形ABCO为正方形,D为OC的中点,
∴OA=AB=BC=CO=4,OD=DC=2,
∠BCO=COA=∠OAB=90°
∵△BCD与△BMD关于BD对称,
∴△BCD≌△BMD
∴∠DMB=∠BCD=90°,DM=DC=DO=2
∠CDB=∠MDB
∵DE=DE
∴Rt△DOE≌Rt△DME
∴∠ODE=∠MDE
∴∠ODE+∠BCD=180°÷2=90°
而∠BCD+∠CBD=90°
∴∠ODE=∠CBD
∴Rt△CBD∽Rt△ODE
∴![]()
∴![]()
(2)有(1)知,D(0,2),E(1,0),设过D,E两点,对称轴为直线![]() 的抛物线的解析式为:
的抛物线的解析式为:![]() ,得
,得
 解之得
解之得
∴![]()
(3)存在点P,使以P、E、D、B为顶点的四边形是梯形,分三种情况讨论:
①当PE∥BD,PE≠BD时,四边形PEDB是梯形.
设直线PE交![]() 轴于点F,易证Rt△DEO∽Rt△EOF
轴于点F,易证Rt△DEO∽Rt△EOF
可得,OF=![]() ,∴F(0,
,∴F(0,![]() )
)
过E,F两点,用待定系数法可求直线PE 的解析式为:![]()
当![]() ,此时P点的坐标为(2,
,此时P点的坐标为(2,![]() )
)
②当PD∥BE,PD≠BE时,四边形PDEB为梯形.
设直线PD交![]() 轴于点G
轴于点G
∵PD∥DE,∴∠GDE=∠DEB
∵∠DEG=∠DEB ∴∠GDE=∠DEG
∴GD=GE,设OG=![]() ,在Rt△DGO中,
,在Rt△DGO中,
![]() ,OD=2,OE=1,
,OD=2,OE=1,
易求![]() ,∴G(-
,∴G(-![]() )
)
过D,G两点用待定系数法可求直线PD 的解析式为:![]()
当![]() ,此时点P的坐标是(2,
,此时点P的坐标是(2,![]() );
);
③当PB∥DE,PB≠DE时,四边形PDEB为梯形.
设直线PD交![]() 轴于点H,
轴于点H,
∵PB∥DE,∴∠DEB=∠EBH, ∠DEO=∠BH0,
∵∠DEO=∠DEB, ∴∠EBH=∠EHB,
∴EB=EH,
在Rt△ABE中,AE=AO-OE=4-1=3,AB=4,
∴BE=5=EH, ∴OH=OE+EH=1+5=6
∴H(6,0)
过B,H两点用待定系数法可求直线PD 的解析式为: ![]()
当![]() ,此时点P的坐标是(2,8);
,此时点P的坐标是(2,8);
综上所述,符合条件的点P有三个,
其坐标分别为(2,![]() ),(2,
),(2,![]() ),(2,8).
),(2,8).

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为
如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为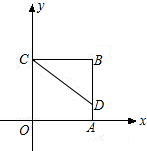 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1. 如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是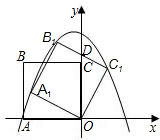 B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.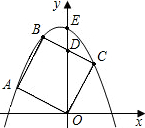 x2+bx+c经过B、C且与y轴的交点为
x2+bx+c经过B、C且与y轴的交点为