��Ŀ����
��ͼ��1������A��2��6����B��m��4���Ƿ���������y=
(x��0)��ͼ�������㣬AC��x�ᣬBD��y�ᣬ����ֱ�ΪC��D��AC��BD�ཻ�ڵ�E������AB��CD��
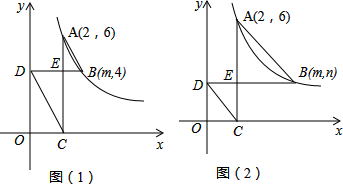
��1�������������ı���ʽΪ
��2����֤��AB��CD��
��3����ͼ��2��������B��m��n����ͼ��1����˫����y=
(x��0)�ϵĶ��㣬��m��2�������������䣮
���ж�AB��CD��λ�ù�ϵ����˵�����ɣ�
���ڵ�B�˶��Ĺ����У�����AD��BC����AD=BC��ֱ��д����B�����꣮
| k |
| x |

��1�������������ı���ʽΪ
y=
| 12 |
| x |
y=
��m��ֵ����| 12 |
| x |
3
3
����2����֤��AB��CD��
��3����ͼ��2��������B��m��n����ͼ��1����˫����y=
| k |
| x |
���ж�AB��CD��λ�ù�ϵ����˵�����ɣ�
���ڵ�B�˶��Ĺ����У�����AD��BC����AD=BC��ֱ��д����B�����꣮
��������1���ɵ�A��2��6����B��m��4���Ƿ���������y=
(x��0)��ͼ�������㣬���Ƚ���A������������ʽ������÷����������ı���ʽ���ٽ�B��m��4�����룬�������m��ֵ��
��2���ɵ�A��B�����꣬��֤��
=
=
������֤�á�AEB�ס�CED����ɵá�EAB=��ECD���̶�֤��AB��CD��
��3�����ɵ�B������Ϊ����m��n������B�ڵ�һ���ޣ�BD��y���ڵ�D����
=
��
=
�����ɵ�B��m��n����˫����y=
�ϣ���֤��
=
������֤�á�AEB�ס�CED����ɵá�EAB=��ECD���̶�֤��AB��CD��
�ڷֱ�ӵ�AD��BC��ƽ��ʱ����ʱ�ı���ABCD�ǵ������Σ��뵱AD��BCʱ����ʱ�ı���ABCD��ƽ���ı��Σ�ȥ������⼴����ô𰸣�
| k |
| x |
��2���ɵ�A��B�����꣬��֤��
| AE |
| EC |
| BE |
| DE |
| 1 |
| 2 |
��3�����ɵ�B������Ϊ����m��n������B�ڵ�һ���ޣ�BD��y���ڵ�D����
| AE |
| EC |
| 6-n |
| n |
| BE |
| DE |
| m-2 |
| 2 |
| 12 |
| x |
| AE |
| EC |
| BE |
| DE |
�ڷֱ�ӵ�AD��BC��ƽ��ʱ����ʱ�ı���ABCD�ǵ������Σ��뵱AD��BCʱ����ʱ�ı���ABCD��ƽ���ı��Σ�ȥ������⼴����ô𰸣�
����⣺��1���ߵ�A��2��6���Ƿ���������y=
(x��0)��ͼ���ϵĵ㣬
��6=
��
��ã�k=12��
�෴���������ı���ʽΪ��y=
��
��B��m��4���Ƿ���������y=
(x��0)��ͼ���ϵĵ㣬
��4=
��
��ã�m=3��
�ʴ�Ϊ��y=
��3��
��2��֤�����ߡ�BDO=��DOC=��OCD=90�㣬
���ı���DOCE�Ǿ��Σ�
�ߵ�A������Ϊ����2��6����
��AC=6��OC=DE=2��
�ߵ�B������Ϊ����3��4����
��BD=3��OD=EC=4��
��BE=BD-DE=1��AE=AC-CE=2��
��
=
=
��
�ߡ�AEB=��CED��
���AEB�ס�CED��
���EAB=��ECD��
��AB��CD��
��3����AB��CD��
�ߵ�B������Ϊ����m��n������B�ڵ�һ���ޣ�BD��y���ڵ�D��
��BD=m��CE=OD=n��
��m��2��
��BE=m-2��AE=6-n��
��
=
��
=
��
�ߵ�B��m��n����˫����y=
�ϣ�
��n=
��
��
=
=
��
��
=
��
�ߡ�AEB=��CED��
���AEB�ס�CED��
���EAB=��ECD��
��AB��CD��
�ڵ�AD��BC��ƽ��ʱ��
��ʱ�ı���ABCD�ǵ������Σ�
��AC=BD����m=BD=6��
���B����������6��2����
��AD��BCʱ����ʱ�ı���ABCD��ƽ���ı��Σ�
��AE=CE=3��
��n=3��
���B����������4��3����
���B����������6��2����4��3����
| k |
| x |
��6=
| k |
| 2 |
��ã�k=12��
�෴���������ı���ʽΪ��y=
| 12 |
| x |
��B��m��4���Ƿ���������y=
| k |
| x |
��4=
| 12 |
| m |
��ã�m=3��
�ʴ�Ϊ��y=
| 12 |
| x |
��2��֤�����ߡ�BDO=��DOC=��OCD=90�㣬
���ı���DOCE�Ǿ��Σ�
�ߵ�A������Ϊ����2��6����
��AC=6��OC=DE=2��
�ߵ�B������Ϊ����3��4����
��BD=3��OD=EC=4��
��BE=BD-DE=1��AE=AC-CE=2��
��
| AE |
| EC |
| BE |
| DE |
| 1 |
| 2 |
�ߡ�AEB=��CED��
���AEB�ס�CED��
���EAB=��ECD��
��AB��CD��
��3����AB��CD��
�ߵ�B������Ϊ����m��n������B�ڵ�һ���ޣ�BD��y���ڵ�D��
��BD=m��CE=OD=n��
��m��2��
��BE=m-2��AE=6-n��
��
| AE |
| EC |
| 6-n |
| n |
| BE |
| DE |
| m-2 |
| 2 |
�ߵ�B��m��n����˫����y=
| 12 |
| x |
��n=
| 12 |
| m |
��
| AE |
| EC |
6-
| ||
|
| m-2 |
| 2 |
��
| AE |
| EC |
| BE |
| DE |
�ߡ�AEB=��CED��
���AEB�ס�CED��
���EAB=��ECD��
��AB��CD��
�ڵ�AD��BC��ƽ��ʱ��
��ʱ�ı���ABCD�ǵ������Σ�
��AC=BD����m=BD=6��
���B����������6��2����
��AD��BCʱ����ʱ�ı���ABCD��ƽ���ı��Σ�
��AE=CE=3��
��n=3��
���B����������4��3����
���B����������6��2����4��3����
���������⿼���˴���ϵ�������������Ľ���ʽ�����뺯���Ĺ�ϵ�����������ε��ж������ʡ�ƽ���ı��������Լ��������ε����ʵ�֪ʶ�������ۺ��Խ�ǿ���ѶȽϴ�ע�����շ���˼�롢��������˼�������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
�����Ŀ
 ��ͼ�������ϵĵ�A��ʾ����Ϊa����a�ľ���ֵ���� ��������
��ͼ�������ϵĵ�A��ʾ����Ϊa����a�ľ���ֵ���� ��������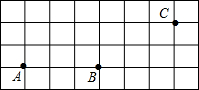 ��ͼ���߶�AB����C�������������У�����С�����εı߳�����ȣ�
��ͼ���߶�AB����C�������������У�����С�����εı߳�����ȣ� ��ͼ��ֱ��DE������A��DE��BC����DAB=78�㣬��ACF=124�㣬���BAC=
��ͼ��ֱ��DE������A��DE��BC����DAB=78�㣬��ACF=124�㣬���BAC= ��ͼ��������ABO�Ƶ�O��ת�õ�������CDO���������ת�����У�
��ͼ��������ABO�Ƶ�O��ת�õ�������CDO���������ת�����У�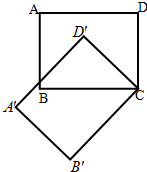 25����ͼ��������ABCD�Ƶ�C����ʱ�뷽����ת45���õ�ͼ��A'B'CD'����ش��������⣺
25����ͼ��������ABCD�Ƶ�C����ʱ�뷽����ת45���õ�ͼ��A'B'CD'����ش��������⣺