题目内容
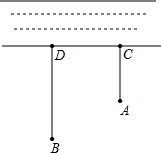 一牧童在A处牧马,牧童的家在B处,A、B处距河岸的距离分别是AC=500m,BD=700m,且C、D两地间距离也为500m,天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
一牧童在A处牧马,牧童的家在B处,A、B处距河岸的距离分别是AC=500m,BD=700m,且C、D两地间距离也为500m,天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
(1)牧童应将马赶到河边的什么地点?请你在图中画出来.
(2)请你求出他至少要走______路程.
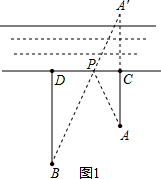 解:(1)作A点关于河岸的对称点A′,连接BA′交河岸与P,
解:(1)作A点关于河岸的对称点A′,连接BA′交河岸与P,则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的P地点.
(2)作DB′=CA′,且DB′⊥CD,
∵DB′=CA′,DB′⊥CD,BB′∥A′A,
∴四边形A′B′BA是矩形,
∴B'A'=CD,
在Rt△BB′A′中,
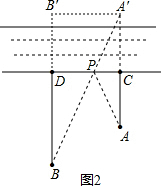
连接A′B′,则BB′=BD+DB′=1200,
BA′=
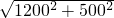 =1300(m).
=1300(m).故答案为:1300m.
分析:(1)将此题转化为轴对称问题,作出A点关于河岸的对称点A′,根据两点之间线段最短得出BA′的长即为牧童要走的最短路程;
(2)根据(1)中所化图象,利用勾股定理解答即可.
点评:此题考查了轴对称--最短路径问题在生活中的应用,要将轴对称的性质和勾股定理灵活应用,体现了数学在解决简单生活问题时的作用.

练习册系列答案
相关题目
 已知,如图,一牧童在A处牧马,牧童家在B处,A,B两处距河岸的距离AC,BD的长分别为700米,500米,且CD的距离为500米,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,那么牧童最少要走
已知,如图,一牧童在A处牧马,牧童家在B处,A,B两处距河岸的距离AC,BD的长分别为700米,500米,且CD的距离为500米,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,那么牧童最少要走 如图,一牧童在A处牧马,牧童家在B处,A、B处距河岸的距离AC、BD的长分别为500m和700m,且C、D两地的距离为500m,天黑前牧童从A点将马牵引到河边去饮水后,再赶回家,那么牧童至少要走( )
如图,一牧童在A处牧马,牧童家在B处,A、B处距河岸的距离AC、BD的长分别为500m和700m,且C、D两地的距离为500m,天黑前牧童从A点将马牵引到河边去饮水后,再赶回家,那么牧童至少要走( )A、100
| ||
| B、1200m | ||
| C、1300m | ||
| D、1700m |
 一牧童在A处牧马,牧童的家在B处,A、B处距河岸的距离分别是AC=500m,BD=700m,且C、D两地间距离也为500m,天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
一牧童在A处牧马,牧童的家在B处,A、B处距河岸的距离分别是AC=500m,BD=700m,且C、D两地间距离也为500m,天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
 已知,如图,一牧童在A处牧马,牧童家在B处,A,B两处距河岸的距离AC,BD的长分别为700米,500米,且CD的距离为500米,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,那么牧童最少要走 米.
已知,如图,一牧童在A处牧马,牧童家在B处,A,B两处距河岸的距离AC,BD的长分别为700米,500米,且CD的距离为500米,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,那么牧童最少要走 米.