Question

已知抛物线y=-x²-x+1与x轴相交于A、B两点（点A在点B的左侧），与y轴交于C点，它的顶点是点D．
（1）求A、B、C、D各点的坐标；
（2）求△ABC的面积；
（3）求四边形ABCD的面积．

Answer 1

解：（1）令y=0得-x²-x+1=0，
求得A（-2-2，0），B（-2+2，0）；
令x=0得C（0，1）；
∵y=-x²-x+1=-（x+2）²+2，
∴D（-2，2）；

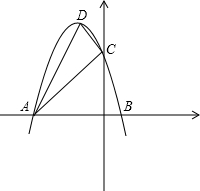
（2）如图
∵AB=（-2+2）-（-2-2）=4，OC=1，
∴S_△ABC=×4×1=2；

（3）S_{四边形ABCD}=×2×2+×（1+2）×2+×1×（-2+2）=2+3．
分析：（1）把抛物线的一般式化成顶点式，让y=0，x=0就可以确定A，B，C，D四个点的坐标了；
（2）求△ABC的面积时，应选AB为底，OA为高求面积；
（3）求四边形ABCD的面积时，用对称轴，y轴把四边形分割成两个直角三角形，一个直角梯形，求它们的面积和．
点评：需熟悉抛物线解析式的三种形式的用途及与坐标轴交点的求法，根据图形进行合理分割，运用相关点的坐标求面积．