Question

关于x的方程有两个不相等的实数根.
(1)求k的取值范围。
(2)是否存在实数k，使方程的两个实数根的倒数和等于0?若存在，求出k的值；若不存在，说明理由

Answer 1

(1)k的取值范围是k＞－1，且k≠0(2) 不存在符合条件的k的值。

解析试题分析：（1）由△=［4(k+2)］²－4×4k·k＞0
∴k＞－1
又∵4k≠0
∴k的取值范围是k＞－1，且k≠0
（2）不存在符合条件的实数k
理由：设方程4kx²+4(k+2)x+k=0的两根分别为x₁、x₂，由根与系数关系有：
x₁+x₂=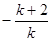，x₁·x₂=，
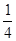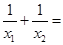
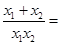
又 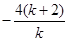=0
∴
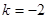
由（1）知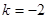，时，△＜0，原方程无实解
∴不存在符合条件的k的值。
考点：一元二次方程
点评：本题难度中等，主要考查学生对一元二次方程知识点的掌握，运用根与系数的关系进行分析为解题关键。