Question

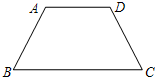如图，等腰梯形ABCD中，AD∥BC，AB=CD．且∠B=60°，AD=AB=4．求梯形ABCD的面积．

Answer 1

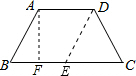解：作DE∥AB交BC与点E．AF⊥BC于点F．
则四边形ABED是平行四边形，△DEC是等边三角形．
∴BE=AD=4，EC=DC=AB=4．
∴BC=BE+EC=4+4=8
在直角△ABF中，AF=AB•sin60°=4×=2，
则梯形的面积是：（AD+BC）•AF=（4+8）×2=12．
分析：作DE∥AB交BC与点E．则四边形ABCD是平行四边形，△DEC是等边三角形，即可求得CD，BE的长度，从而求解．
点评：本题考查等腰梯形的有关计算，正确作出辅助线，转化成平行四边形与等边三角形是关键．