题目内容
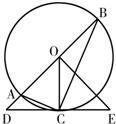 30、如图,直线DE经过⊙O上的点C,并且OE=OD,EC=DC,⊙O交直线OD于A、B两点,连接BC,AC,OC.求证:
30、如图,直线DE经过⊙O上的点C,并且OE=OD,EC=DC,⊙O交直线OD于A、B两点,连接BC,AC,OC.求证:(1)OC⊥DE;
(2)△ACD∽△CBD.
分析:(1)△ODE是等腰三角形,要证OC⊥DE,只要根据等腰三角形的三线合一定理,转化为证明C是底边DE上的中点即可.
(2)要证明△ACD∽△CBD只要求证∠DCA=∠B和∠ADC=∠CDB就可以.
(2)要证明△ACD∽△CBD只要求证∠DCA=∠B和∠ADC=∠CDB就可以.
解答:证明:(1)∵OE=OD,
∴△ODE是等腰三角形.(1分)
∵EC=DC,
∴C是底边DE上的中点.
∴OC⊥DE.(3分)
(2)∵AB是直径,
∴∠ACB=90°.
∴∠B+∠BAC=90°.(4分)
∵∠DCA+∠ACO=90°,∠ACO=∠BAC,
∴∠DCA=∠B.
∵∠ADC=∠CDB,(5分)
∴△ACD∽△CBD.(6分)
∴△ODE是等腰三角形.(1分)
∵EC=DC,
∴C是底边DE上的中点.
∴OC⊥DE.(3分)
(2)∵AB是直径,
∴∠ACB=90°.
∴∠B+∠BAC=90°.(4分)
∵∠DCA+∠ACO=90°,∠ACO=∠BAC,
∴∠DCA=∠B.
∵∠ADC=∠CDB,(5分)
∴△ACD∽△CBD.(6分)
点评:本题主要考查了等腰三角形的三线合一定理,以及相似三角形的判定方法,可以证明两个角对应相等.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 3、如图,直线DE经过点A,DE∥BC,∠B=60°,下列结论成立的是( )
3、如图,直线DE经过点A,DE∥BC,∠B=60°,下列结论成立的是( )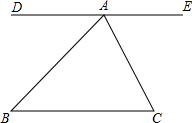 如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=57°.
如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=57°. 如图,直线DE经过点A,DE∥BC,∠DAB=78°,∠ACF=124°,则∠BAC=
如图,直线DE经过点A,DE∥BC,∠DAB=78°,∠ACF=124°,则∠BAC=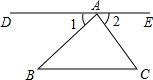 如图,直线DE经过点A,DE∥BC,若∠B=45°,∠C=55°.
如图,直线DE经过点A,DE∥BC,若∠B=45°,∠C=55°.