Question

已知△ABC中,∠A=60°,BC=a,AC=b,AB=c,AP是BC边上的中线,则AP 的长是(   ).

    (A);(B);(C);(D)

Answer 1

如图延长中线AP到E,使PE=AP,连接EB,可得△ABC≌△APC,∴∠E=∠PAC, BE=AC=b.

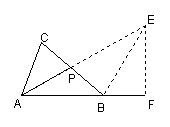    ∴∠PAB+∠E=∠CAB=60°

    ∴ ∠ABE=120°;

    作EF⊥AB延长线于F,∴∠EBF=180°-120°=60°

    ∴ ∠BEF=30⁰   ∴BF=BE=b.

    在Rt△BEF中,根据勾股定理:EF²=b²+.

    在Rt△AEF中,根据勾股定理:AE=.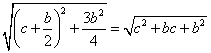

    ∴ PA=AE=.    选(B)