Question

【题目】在中，为的角平分线.

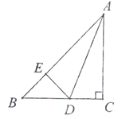
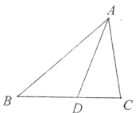
图1 图2

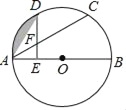
（1）如图1，，，点在边上，，请直接写出图中所有与相等的线段.

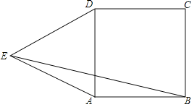
（2）如图2，，如果，求证：.

Answer 1

【答案】（1）=；（2）证明见解析．

【解析】

（1）根据角平分线的性质结合已知条件可证得，再证得，从而证得=；

（2）在AB上取点E，使得AE=AC，则可证得△AED≌△ACD，可得∠AED=∠C=2∠B，ED=CD，可证得△BDE为等腰三角形，所以有BE=DE=CD，可得结论．

（1）∵为的角平分线，

∴∠EAD=∠CAD，

∵，

在△AED和△ACD中，，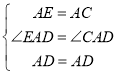

∴，

∴，，

∵，

∴，

∵，

∴，

∴，

∴=；

（2）在AB上取点E，使得AE=AC，

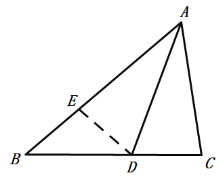
在△AED和△ACD中

∴△AED≌△ACD（SAS），
∴∠AED=∠C， ED=CD，
∵∠C=2∠B，

又∠AED=∠B+∠BDE=2∠B，
∴∠B=∠BDE，
∴BE=DE，
∴AB=AE+BE=AC+DE=AC+CD．