题目内容
如图所示，四边形ABCD是平行四边形，AB=13，AD=5，AC⊥BC，则S?ABCD=________．
60
分析：根据平行四边形的性质以及勾股定理求出四边形ABCD的底边BC和其对角线AC的值，然后根据平行四边形的面积计算公式求解．
解答：∵四边形ABCD为平行四边形，
∴BC=AD=5．
∵AC⊥BC，
∴△ACB是直角三角形．
∴AC=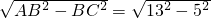
=12．
∴S?ABCD=BC•AC=5×12=60．
故答案为60．
点评：本题直接通过平行四边形性质和勾股定理以及平行四边形的面积公式解决．平行四边形的面积等于平行四边形的边长与该边上的高的积．即S=a•h．其中a可以是平行四边形的任何一边，h必须是a边与其对边的距离，即对应的高．
分析：根据平行四边形的性质以及勾股定理求出四边形ABCD的底边BC和其对角线AC的值，然后根据平行四边形的面积计算公式求解．
解答：∵四边形ABCD为平行四边形，
∴BC=AD=5．
∵AC⊥BC，
∴△ACB是直角三角形．
∴AC=
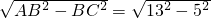=12．∴S?ABCD=BC•AC=5×12=60．
故答案为60．
点评：本题直接通过平行四边形性质和勾股定理以及平行四边形的面积公式解决．平行四边形的面积等于平行四边形的边长与该边上的高的积．即S=a•h．其中a可以是平行四边形的任何一边，h必须是a边与其对边的距离，即对应的高．
练习册系列答案
相关题目
21、如图所示，四边形ABCD是平行四边形，E，F分别在AD，CB的延长线上，且DE=BF，连接FE分别交AB，CD于点H，G．
12、如图所示，四边形ABCD为⊙O的内接四边形，E为AB延长线的上一点，∠CBE=40°，则∠AOC等于（ ）
如图所示，四边形ABCD中，E、F分别为AD、BC的中点．
