题目内容
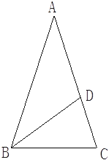
【题目】如图，梯形ABCD中，AD∥BC，∠D=90°，BC=CD=12，∠ABE=45°，点E在DC上，AE，BC的延长线相交于点F，若AE=10，则S△ADE+S△CEF的值是______ .
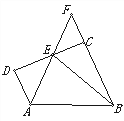
【答案】30或48
【解析】
如图，首先把梯形补成正方形，然后把△BEC旋转到△BMN的位置，根据它们条件容易证明：△ANB和△ABE全等，故AE=AN=10，设CE=x，然后用x表示AM，AD，DE在根据△ADE是直角三角形利用勾股定理建立关于x的方程，解方程求出x，就可以求出S△ADE+S△CEF的值．
如图，延长DA，过B作BM⊥DA，交其延长线于M．
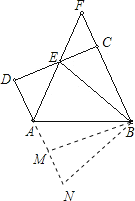
∴四边形DCBM是正方形，
∴DM=BC=CD=12，再把△BEC旋转到△BMN的位置，
∴BN=BE，∠EBC=∠MBN，CE=MN
∵∠ABE=45°
∴∠EBC+∠ABM=90°-45°=45°
∴∠ABN=∠ABM+∠MBN=45°，AB公共
∴△ABN≌△ABE
∴AN=AE=10，设CE=x，那么MN=x，DE=CD-CE=12-x，AM=10-x，AD=12-AM=2+x，
在Rt△ADE中：AD2+DE2=AE2
∴（2+x）2+（12-x）2=102
∴x1=4，x2=6，
当x=4时，CE=4，DE=8，AD=6
∵AD∥CF
∴△ADE∽△FCE，
∴
，
∴CF=3，
∴S△ADE+S△CEF=30；
当x=6时，CE=6，DE=6，AD=8
∵AD∥CF
∴△ADE∽△FCE
∴，
∴CF=8
∴S△ADE+S△CEF=48．
综上所述，S△ADE+S△CEF的值是30或48．
故答案为：30或48．
练习册系列答案
相关题目
