题目内容
如图所示,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,若∠AOC=68°,则∠BOF和∠EOF是多少度?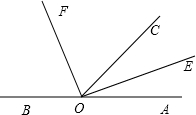
分析:由角平分线的定义,结合平角的定义,易求∠BOF和∠EOF的度数.
解答:解:点O是直线AB上一点,则∠AOB=180°,
若∠AOC=68°,
则∠BOC=∠AOB-∠AOC=180°-68°=112°,
∵OF平分∠BOC,
∴∠BOF=
∠BOC=
×112°=56°;
又∵OE平分∠AOC,
∴∠EOF=
∠AOC+
∠BOC=34°+56°=90°.
故∠BOF和∠EOF分别是56°和90°.
若∠AOC=68°,
则∠BOC=∠AOB-∠AOC=180°-68°=112°,
∵OF平分∠BOC,
∴∠BOF=
| 1 |
| 2 |
| 1 |
| 2 |
又∵OE平分∠AOC,
∴∠EOF=
| 1 |
| 2 |
| 1 |
| 2 |
故∠BOF和∠EOF分别是56°和90°.
点评:根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
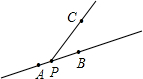 如图所示,点P是直线AB上的一个运动点,点C是直线AB外一固定的点,则下列描述正确的是( )
如图所示,点P是直线AB上的一个运动点,点C是直线AB外一固定的点,则下列描述正确的是( )| A、在点P的运动过程中,使直线PC⊥AB的点P有两个 | B、若∠CBA>90°,当点P从A出发,沿射线AB的方向运动时,∠CPB不断变大 | C、若AB=2AP,则点P是线段AB的中点 | D、当∠CPA=90°时,线段CP的长度就是点C到直线AB的距离 |
 解:∵O是直线AB上一点
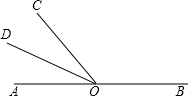
解:∵O是直线AB上一点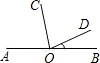 如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,则∠AOC=
如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,则∠AOC=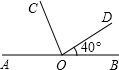 如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=40°,则∠AOC=
如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=40°,则∠AOC=