题目内容
设二次函数y=ax2+bx+c的图象开口向下,顶点落在第二象限.(1)确定a,b,b2-4ac的符号,简述理由.
(2)若此二次函数图象经过原点,且顶点在直线x+y=0上,顶点与原点的距离为3
| 2 |
分析:(1)根据抛物线的开口向下判断a的符号,再根据第二象限点的坐标特点及二次函数的顶点坐标列出不等式组解答.
(2)根据抛物线过原点及顶点在直线x+y=0上求出其顶点坐标及一次项系数,再根据顶点与原点的距离为3
求出二次项系数,进而求出其解析式.
(2)根据抛物线过原点及顶点在直线x+y=0上求出其顶点坐标及一次项系数,再根据顶点与原点的距离为3
| 2 |
解答:解:(1)抛物线开口向下,所以a<0;(2分)
顶点在第二象限,所以
,b<0,b2-4ac>0.(4分)
(2)由题意可得c=0,(8分)
此时顶点坐标为(-
,-
),因顶点在直线x+y=0上,
所以-
-
=0,b=-2.(11分)
此时顶点坐标为(
,-
),由
+
=18,a=-
,(14分)
抛物线的解析式为y=-
x2-2x.(16分)
顶点在第二象限,所以
|
(2)由题意可得c=0,(8分)
此时顶点坐标为(-
| b |
| 2a |
| b2 |
| 4a |
所以-
| b |
| 2a |
| b2 |
| 4a |
此时顶点坐标为(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| 3 |
抛物线的解析式为y=-
| 1 |
| 3 |
点评:本题考查的是二次函数的图象与系数的关系及用待定系数法求二次函数的解析式,有一定的难度.

练习册系列答案
相关题目
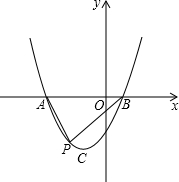 三点,且满足y12=y22=y32=1.
三点,且满足y12=y22=y32=1.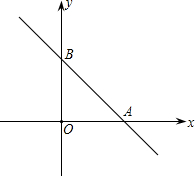 an∠OAB=2.二次函数y=ax2+bx+2的图象经过点A、B,顶点为D,对称轴为x=3.
an∠OAB=2.二次函数y=ax2+bx+2的图象经过点A、B,顶点为D,对称轴为x=3. 设二次函数y1=x2-4x+3的图象为C1,二次函数y2=ax2+bx+c(a≠0)的图象与C1关于y轴对称.
设二次函数y1=x2-4x+3的图象为C1,二次函数y2=ax2+bx+c(a≠0)的图象与C1关于y轴对称.