��Ŀ����
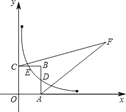
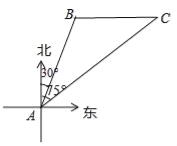
����Ŀ����ͼ��1����ʾ��һ�ܳ�4������ABб���������OM��ֱ��ǽ��ON�ϣ�������������ɵĽ�Ϊ60��.
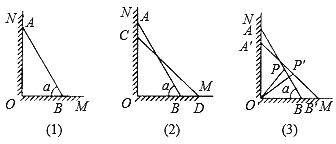
��1����ͼ��1���е�AO��BO�ij��ȣ�
��2�������Ӷ���A��NO�»���ͬʱ��B��OM���һ���.
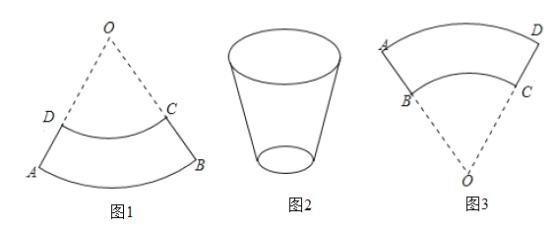
����ͼ��2����ʾ����A���»���C�㣬B�����һ��е�D�㣬����AC:BD2:3�������AC�ij��ȣ�
����ͼ��3����ʾ����A���»���A�㣬B�����һ��е�B��ʱ������AB���е�PҲ��֮�˶���P�㣬��POP15������AA�ij���.
���𰸡���1��OA 2![]() ��OB 2����2����
��OB 2����2����![]() �ף���
�ף���![]() ��.
��.
��������
��1�����ݺ�30����ֱ�������ε����ʼ������;��2������ AC 2x, BD 3x����Rt��MOC�и��ݹ��ɶ�����ʽ�������x�������AC�ij��������P'OM 60 15 45����OP' M Ϊ����ֱ�������Σ����ɸ��������ʽ������.
�⣺��1���ߡ�=60�������OAB=30����
��OB 2��OA 2![]()
��2���� AC 2x, BD 3x ��
�ɵ�![]() ��
��
�ã� x1 0(��),![]() ��
��
���� ![]() �ס�
�ס�
��3����ΪP'OM 60 15 45 �� P'O P' M ��
OP' M Ϊ����ֱ�������Σ�
��![]()
![]() ��.
��.

��ϰ��ϵ�д�
�����Ŀ